题目
已知方阵满足 则 的逆矩阵是
已知方阵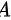 满足
满足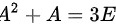 则
则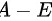 的逆矩阵是
的逆矩阵是
题目解答
答案
答: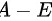 的逆矩阵是
的逆矩阵是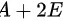 .
.
解析:根据题意得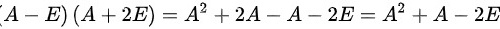
所以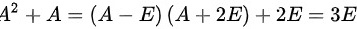
可得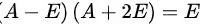
因此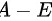 的逆矩阵为
的逆矩阵为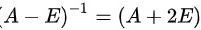
解析
考查要点:本题主要考查矩阵的逆矩阵求解,以及利用已知矩阵方程进行代数变形的能力。
解题核心思路:
题目给出方阵$A$满足$A^2 + A = 3E$,需要求矩阵$(A - E)$的逆矩阵(题目中可能笔误为“H-V”)。
关键点在于构造乘积$(A - E)(A + 2E)$,通过代入已知条件$A^2 + A = 3E$,验证该乘积是否为单位矩阵$E$,从而确定逆矩阵。
步骤1:展开乘积
计算$(A - E)(A + 2E)$:
$\begin{aligned}(A - E)(A + 2E) &= A \cdot A + 2A \cdot E - E \cdot A - 2E \cdot E \\&= A^2 + 2A - A - 2E \\&= A^2 + A - 2E.\end{aligned}$
步骤2:代入已知条件
题目给出$A^2 + A = 3E$,代入上式:
$A^2 + A - 2E = 3E - 2E = E.$
步骤3:结论
因此,$(A - E)(A + 2E) = E$,说明$A + 2E$是$(A - E)$的逆矩阵,即:
$(A - E)^{-1} = A + 2E.$