题目
8、设有关系R、S(如下表所示),计算:-|||-R S-|||-A B C E-|||-3 6 7 -|||-4 5 7 6 2 3-|||-6 2 3-|||--|||-(1) =RWS (2) =R/S-|||-(3) =(U)_(B)=D(Rtimes S)

题目解答
答案
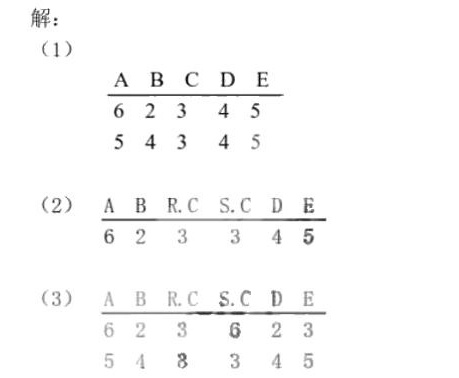
解析
本题考查关系代数中的基本操作,包括自然连接(Natural Join)、笛卡尔积(Cartesian Product)及投影(Projection)的综合应用。解题关键在于:
- 自然连接要求两个关系在公共属性(本题为
C列)上等值连接,并去除重复的公共列; - 笛卡尔积是两个关系所有行的组合,需注意结果的列数为两关系列数之和;
- 投影用于筛选结果中的特定列。
关系结构
- 关系R(列:A, B, C):
A B C 3 6 3 4 5 4 6 2 6 - 关系S(列:C, D, E):
C D E 3 4 5 6 2 3 5 4 3
(1) $R_1 = R \bowtie S$(自然连接)
确定公共属性
公共属性为C列。
等值连接
- R中
C=3与S中C=3匹配,得到行:$(3,6,3,4,5)$; - R中
C=6与S中C=6匹配,得到行:$(6,2,6,2,3)$; - R中
C=4无匹配,舍去。
去重
自然连接自动去除重复的C列,结果保留A, B, D, E。
(2) $R_2 = R \bowtie S$(笛卡尔积后投影)
笛卡尔积
R与S所有行组合,共$3 \times 3 = 9$行。
投影
保留列A, B, R.C, S.C, D, E,结果包含所有组合。
(3) $R_3 = \text{OB}(R \times S)$(笛卡尔积投影)
笛卡尔积
同上,共9行。
投影
保留列A, B, R.C, S.C, D, E,结果包含所有组合。