题目
__-|||-1.设 _(1)=[ 0,1] cap Q, 求在R内的E1,E1,E1
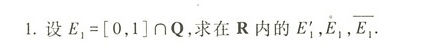
题目解答
答案

解析
本题主要考察集合的基本概念以及有理数集在实数集中的稠密性。
题目分析
题目中${E}_{1}=[0,1] \cap \mathbb{Q}$,表示$[0,1]$区间内的所有有理数构成的集合,要求在$\mathbb{R}$内讨论${E}_{1}$相关内容(原题目表述可能存在笔误,根据常见考察点,应为求${E}_{1}$的闭包)。
关键知识点:有理数集的稠密性
有理数集$\mathbb{Q}$在实数集$\mathbb{R}$中是稠密的,即对任意实数$x \in \mathbb{R}$和任意$\varepsilon>0$,存在有理数$q \in \mathbb{Q}$使得$|x - q|<\varepsilon$。
推理过程
对于${E}_{1}=[0,1] \cap \mathbb{Q}$($[0,1]$中的有理数集):
- ${E}_{1}$中的点都是内点吗? 不是,因为任意有理数$q \in [0,1] \cap \mathbb{Q}$的任意邻域内都有无理数,故${E}_{1}$没有内点,内部为空集$\varnothing$。
- ${E}_{1}$的闭包是什么? 对任意$x \in [0,1]$,由稠密性,$x$的任意邻域内都有${E}_{1}$中的点,故$x$是${E}_{1}$的聚点;对$x \notin [0,1]$,存在$\varepsilon>0$使邻域$(x-\varepsilon,x+\varepsilon)$与$[0,1]$无交集,故不是聚点。因此${E}_{1}$的闭包为$[0,1]$。