题目
求lim _(xarrow infty )xsin dfrac (2)(x)
求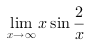
题目解答
答案
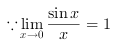
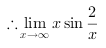
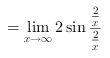
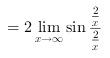
=2
解析
考查要点:本题主要考查无穷小量的等价替换以及变量替换法在极限计算中的应用。关键在于将原式转化为已知的极限形式。
解题核心思路:当$x \rightarrow \infty$时,$\dfrac{2}{x} \rightarrow 0$,此时$\sin \dfrac{2}{x}$可以近似为$\dfrac{2}{x}$(等价无穷小替换)。通过这一替换,原式可简化为容易计算的形式。
破题关键点:
- 识别等价无穷小:当$t \rightarrow 0$时,$\sin t \sim t$。
- 变量替换:令$t = \dfrac{1}{x}$,将$x \rightarrow \infty$转化为$t \rightarrow 0$,简化表达式。
步骤1:变量替换
令$t = \dfrac{1}{x}$,则当$x \rightarrow \infty$时,$t \rightarrow 0$。原式可改写为:
$\lim_{x \rightarrow \infty} x \sin \dfrac{2}{x} = \lim_{t \rightarrow 0} \dfrac{\sin 2t}{t}$
步骤2:应用等价无穷小替换
当$t \rightarrow 0$时,$\sin 2t \sim 2t$,因此:
$\lim_{t \rightarrow 0} \dfrac{\sin 2t}{t} = \lim_{t \rightarrow 0} \dfrac{2t}{t} = \lim_{t \rightarrow 0} 2 = 2$
结论:原式的极限值为$2$。