题目
1.计算下列极限:-|||-(13) lim _(narrow infty )dfrac ((n+1)(n+2)(n+3))(5{n)^3};

题目解答
答案
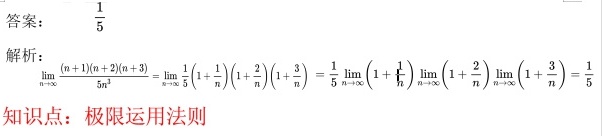
解析
考查要点:本题主要考查多项式分式极限的计算方法,特别是当变量趋向于无穷大时,如何通过分析最高次项的系数比值来确定极限值。
解题核心思路:
当分子和分母均为多项式时,最高次项的系数比值通常决定了极限的结果。对于分式极限,可以将分子和分母的最高次项提取出来,或通过展开分子后化简,最终利用极限的运算性质求解。
破题关键点:
- 识别分子展开后的最高次项:分子 $(n+1)(n+2)(n+3)$ 展开后为 $n^3 + 6n^2 + 11n + 6$,最高次项为 $n^3$。
- 比较分子与分母的最高次项系数:分子最高次项系数为 $1$,分母为 $5n^3$,系数为 $5$,因此极限值为 $\frac{1}{5}$。
步骤1:展开分子
将分子 $(n+1)(n+2)(n+3)$ 展开:
- 先计算前两个括号:
$(n+1)(n+2) = n^2 + 3n + 2$ - 再乘以第三个括号:
$(n^2 + 3n + 2)(n+3) = n^3 + 6n^2 + 11n + 6$
步骤2:化简分式
原式可写为:
$\frac{n^3 + 6n^2 + 11n + 6}{5n^3}$
将分子和分母同时除以 $n^3$:
$\frac{1 + \frac{6}{n} + \frac{11}{n^2} + \frac{6}{n^3}}{5}$
步骤3:取极限
当 $n \rightarrow \infty$ 时,$\frac{6}{n}$、$\frac{11}{n^2}$、$\frac{6}{n^3}$ 均趋向于 $0$,因此极限值为:
$\frac{1 + 0 + 0 + 0}{5} = \frac{1}{5}$