题目
设二维随机变量(X,Y)的概率分布如下:Y-|||-x 1 2 3-|||-1 0.15 0.25 0.10-|||-5 0.15 0.25 0.10则P(X=1)为()A 0.5 B 0C 1D 0.4
设二维随机变量(X,Y)的概率分布如下:
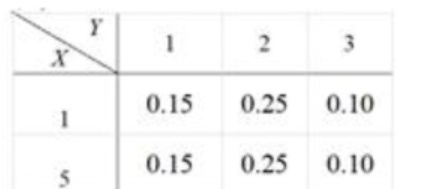
则P(X=1)为()
A 0.5
B 0
C 1
D 0.4
题目解答
答案
1. 首先分析题目:
题目给出了二维随机变量(X,Y)的概率分布表。
要求计算P(X = 1)。
2. 计算P(X = 1):
根据概率分布表,X = 1时,对应的Y有三种情况: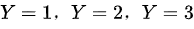 。
。
我们需要将X = 1对应的所有概率相加。
从表中可以看出:
当X = 1且Y = 1时,概率为0.15。
当X = 1且Y = 2时,概率为0.25。
当X = 1且Y = 3时,概率为0.10。
3. 求和:
P(X = 1)=0.15 + 0.25+0.10 = 0.5
所以,答案是A选项。
解析
步骤 1:理解题目
题目给出了二维随机变量(X,Y)的概率分布表。要求计算P(X = 1)。
步骤 2:计算P(X = 1)
根据概率分布表,X = 1时,对应的Y有三种情况:Y=1, Y=2, Y=3。我们需要将X = 1对应的所有概率相加。
从表中可以看出:
当X = 1且Y = 1时,概率为0.15。
当X = 1且Y = 2时,概率为0.25。
当X = 1且Y = 3时,概率为0.10。
步骤 3:求和
P(X = 1) = 0.15 + 0.25 + 0.10 = 0.5
题目给出了二维随机变量(X,Y)的概率分布表。要求计算P(X = 1)。
步骤 2:计算P(X = 1)
根据概率分布表,X = 1时,对应的Y有三种情况:Y=1, Y=2, Y=3。我们需要将X = 1对应的所有概率相加。
从表中可以看出:
当X = 1且Y = 1时,概率为0.15。
当X = 1且Y = 2时,概率为0.25。
当X = 1且Y = 3时,概率为0.10。
步骤 3:求和
P(X = 1) = 0.15 + 0.25 + 0.10 = 0.5