题目
设事件A与B互不相容,且0<P(B)<1,证明:(A|overline (B))=dfrac (P(A))(1-P(B))
设事件A与B互不相容,且0<P(B)<1,证明:
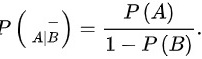
题目解答
答案
解:由条件概率公式:
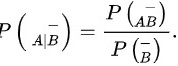 由于A与B互不相容,所以有P(AB)=0,且
由于A与B互不相容,所以有P(AB)=0,且
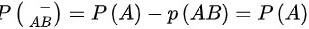 ,
,
又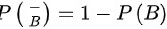
从而有:
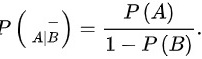
解析
考查要点:本题主要考查条件概率的计算以及互不相容事件的性质。
解题核心思路:利用事件互不相容的性质,确定事件$A$与$\overline{B}$的关系,结合条件概率公式进行推导。
破题关键点:
- 互不相容事件的定义:$P(AB)=0$,即$A$和$B$不能同时发生。
- 事件包含关系:由于$A$与$B$互不相容,$A$必然包含在$\overline{B}$中,因此$A \cap \overline{B} = A$。
- 条件概率公式:$P(A|\overline{B}) = \dfrac{P(A \cap \overline{B})}{P(\overline{B})}$。
步骤1:明确条件概率公式
根据条件概率的定义:
$P(A|\overline{B}) = \dfrac{P(A \cap \overline{B})}{P(\overline{B})}$
步骤2:利用互不相容性质简化分子
由于$A$与$B$互不相容,即$P(AB)=0$,因此:
$A \cap \overline{B} = A \quad \text{(因为$A$不可能与$B$同时发生)}$
故分子可化简为:
$P(A \cap \overline{B}) = P(A)$
步骤3:计算分母
$\overline{B}$的概率为:
$P(\overline{B}) = 1 - P(B)$
步骤4:代入公式得结论
将分子和分母代入条件概率公式:
$P(A|\overline{B}) = \dfrac{P(A)}{1 - P(B)}$