下面哪个逻辑等价关系是不成立的()A. |x-P(x)= -∃xP(x)B. |x-P(x)= -∃xP(x)C. |x-P(x)= -∃xP(x)D. |x-P(x)= -∃xP(x)
下面哪个逻辑等价关系是不成立的()
A. 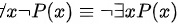
B. 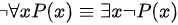
C. 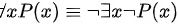
D. 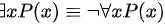
题目解答
答案
首先,我们回顾逻辑等价的定义:如果两个命题在逻辑上总是同时为真或同时为假,那么这两个命题是逻辑等价的。
现在,我们逐一分析每个选项:
A. 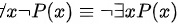
左边表示对于所有x,P(x)都不成立。
右边表示不存在一个x使得P(x)成立。
这两个命题是逻辑等价的,因为“对于所有x都不成立”等价于“不存在一个x成立”。
B. 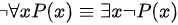
左边表示不是对于所有x,P(x)都成立,即存在至少一个x使得P(x)不成立。
右边表示存在一个x使得P(x)不成立。
这两个命题也是逻辑等价的。
C. 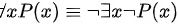
左边表示对于所有x,P(x)都成立。
右边表示不存在一个x使得P(x)不成立,即对于所有x,P(x)都成立。
这两个命题同样是逻辑等价的。
D. 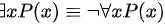
左边表示存在一个x使得P(x)成立。
右边表示不是对于所有x,P(x)都成立,即存在至少一个x使得P(x)不成立。
这两个命题不是逻辑等价的。左边只是说存在一个x满足P(x),而右边则说至少有一个x不满足P(x),它们可能在某些情况下同时为真,但在其他情况下可能一个为真而另一个为假。
综上所述,不成立的逻辑等价关系是D选项。
解析
逻辑等价关系的核心在于判断两个命题是否在所有情况下具有相同的真值。本题需识别四个选项中不成立的等价关系。关键点在于:
- 德摩根定律对量词的转换规则;
- 存在量词与全称量词的否定关系;
- 命题间的蕴含与矛盾关系。
选项A:$\forall x \neg P(x) \equiv \neg \exists x P(x)$
- 左边表示“所有x都不满足P(x)”。
- 右边表示“不存在x使得P(x)成立”。
- 根据德摩根定律,$\neg \exists x P(x) \equiv \forall x \neg P(x)$,两者等价。
选项B:$\neg \forall x P(x) \equiv \exists x \neg P(x)$
- 左边表示“并非所有x都满足P(x)”。
- 右边表示“存在x不满足P(x)”。
- 根据德摩根定律,$\neg \forall x P(x) \equiv \exists x \neg P(x)$,两者等价。
选项C:$\forall x P(x) \equiv \neg \exists x \neg P(x)$
- 左边表示“所有x都满足P(x)”。
- 右边表示“不存在x不满足P(x)”。
- 两者互为否定的否定,等价成立。
选项D:$\exists x P(x) \equiv \neg \forall x P(x)$
- 左边表示“存在x满足P(x)”。
- 右边表示“并非所有x都满足P(x)”。
- 关键矛盾:若所有x都满足P(x),则左边为真,右边为假;若仅部分x满足P(x),两者可能同时为真。因此,两者并非逻辑等价。