问f(z)=x+2yi是否可导?
问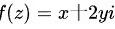 是否可导?
是否可导?
题目解答
答案
解:

解析
考查要点:本题主要考查复变函数的可导性条件,即柯西-黎曼方程的应用。
解题核心思路:
将函数$f(z)=x+2yz$分解为实部$u(x,y)$和虚部$v(x,y)$,代入柯西-黎曼方程,验证是否在复平面内存在满足条件的点。若仅在孤立点满足,则函数不可导。
破题关键点:
- 正确展开函数表达式,将$yz$用$y(x+iy)$替换;
- 分离实部和虚部,得到$u$和$v$的表达式;
- 计算偏导数,代入柯西-黎曼方程,分析解的存在性。
将函数$f(z)=x+2yz$展开:
设$z=x+iy$,则$yz=y(x+iy)=xy+iy^2$,代入原函数得:
$f(z)=x+2(yz)=x+2(xy+iy^2)=x+2xy+i2y^2.$
分离实部和虚部:
$u(x,y)=x+2xy, \quad v(x,y)=2y^2.$
柯西-黎曼方程要求:
$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}.$
计算偏导数:
-
$\frac{\partial u}{\partial x} = 1 + 2y$,$\frac{\partial v}{\partial y} = 4y$;
代入第一个方程得:
$1 + 2y = 4y \quad \Rightarrow \quad y = \frac{1}{2}.$ -
$\frac{\partial u}{\partial y} = 2x$,$\frac{\partial v}{\partial x} = 0$,故$-\frac{\partial v}{\partial x}=0$;
代入第二个方程得:
$2x = 0 \quad \Rightarrow \quad x = 0.$
结论:
柯西-黎曼方程仅在点$(0, \frac{1}{2})$处成立,但该点周围不满足条件,因此$f(z)$在复平面内不可导。