题目
3.求通过两条平行直线_(1):dfrac (x-1)(2)=dfrac (y-2)(-1)=dfrac (z+3)(1) 和 _(2):dfrac (x-3)(2)=dfrac (y-4)(-1)=dfrac (z-2)(1)的平面方程。
3.求通过两条平行直线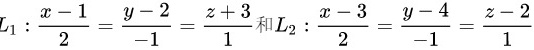
的平面方程。
题目解答
答案
两条直线的方向向量均为v=(2,-1,1).
点v1 =( 1, 2, -3),点v2 =(3, 4, 2),两点构成给方向向量v3=(2,2,5).
然后,我们可以通过计算v3和方向向量的叉积得到平面的法向量。
法向量n = v× v3
=(7,8,2)
最后,我们可以使用点法式(点法向式)得到平面方程。选择L1上的一个点(1, 2, -3),用法向量n表示平面方程:
7(x-1) +8 (y-2) -2(z+3) = 0
化简得到平面方程:
7x + 8y -2z + 29 = 0
解析
步骤 1:确定直线的方向向量
两条直线的方向向量均为v=(2,-1,1)。
步骤 2:确定平面上的两个点
点v1 =( 1, 2, -3),点v2 =(3, 4, 2)。这两个点分别位于两条平行直线上。
步骤 3:计算平面上的两个向量
由点v1和点v2可以得到向量v3=(2,2,5)。
步骤 4:计算平面的法向量
法向量n = v× v3
=(7,8,2)
步骤 5:使用点法式得到平面方程
选择L1上的一个点(1, 2, -3),用法向量n表示平面方程:
7(x-1) +8 (y-2) -2(z+3) = 0
化简得到平面方程:
7x + 8y -2z + 29 = 0
两条直线的方向向量均为v=(2,-1,1)。
步骤 2:确定平面上的两个点
点v1 =( 1, 2, -3),点v2 =(3, 4, 2)。这两个点分别位于两条平行直线上。
步骤 3:计算平面上的两个向量
由点v1和点v2可以得到向量v3=(2,2,5)。
步骤 4:计算平面的法向量
法向量n = v× v3
=(7,8,2)
步骤 5:使用点法式得到平面方程
选择L1上的一个点(1, 2, -3),用法向量n表示平面方程:
7(x-1) +8 (y-2) -2(z+3) = 0
化简得到平面方程:
7x + 8y -2z + 29 = 0