题目
1.求方程 dfrac (dy)(dx)=x+(y)^2 通过点(0,0)的第三次近似解.

题目解答
答案
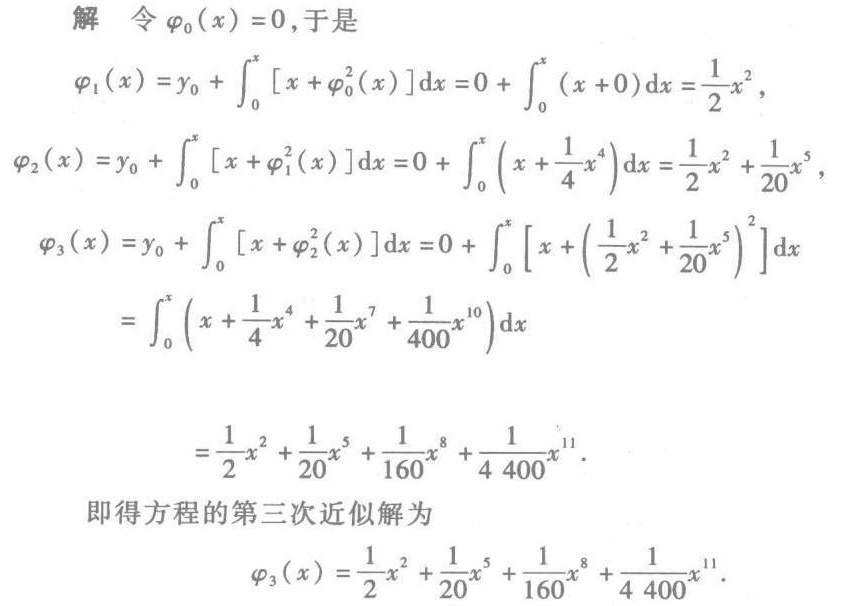
解析
考查要点:本题主要考查逐次逼近法(Picard迭代法)的应用,用于求解微分方程的近似解。需要掌握如何通过迭代构造近似解序列,并逐步逼近真实解。
解题核心思路:
- 初始猜测:从初始条件出发,选择最简单的函数作为初始近似解(通常为常数函数)。
- 迭代公式:将微分方程转化为积分方程,代入前一次的近似解,计算出下一次的近似解。
- 逐次逼近:通过多次迭代,逐步提高近似解的精度,直到达到所需的近似次数(本题为第三次)。
破题关键点:
- 正确展开平方项:在每次迭代中,需将前一次的近似解平方后展开,注意多项式的乘法运算。
- 准确积分:对展开后的多项式逐项积分,确保系数计算无误。
1. 初始近似解
根据初始条件 $y(0)=0$,选择初始近似解为:
$\varphi_0(x) = 0$
2. 第一次迭代(φ₁(x))
将 $\varphi_0(x)=0$ 代入积分方程:
$\varphi_1(x) = \int_0^x \left[ t + \varphi_0(t)^2 \right] dt = \int_0^x t \, dt = \frac{1}{2}x^2$
3. 第二次迭代(φ₂(x))
将 $\varphi_1(x)=\frac{1}{2}x^2$ 代入积分方程:
$\varphi_2(x) = \int_0^x \left[ t + \left( \frac{1}{2}t^2 \right)^2 \right] dt = \int_0^x \left( t + \frac{1}{4}t^4 \right) dt = \frac{1}{2}x^2 + \frac{1}{20}x^5$
4. 第三次迭代(φ₃(x))
将 $\varphi_2(x)=\frac{1}{2}x^2 + \frac{1}{20}x^5$ 代入积分方程:
- 展开平方项:
$\left( \frac{1}{2}x^2 + \frac{1}{20}x^5 \right)^2 = \frac{1}{4}x^4 + \frac{1}{20}x^7 + \frac{1}{400}x^{10}$ - 积分计算:
$\varphi_3(x) = \int_0^x \left( t + \frac{1}{4}t^4 + \frac{1}{20}t^7 + \frac{1}{400}t^{10} \right) dt$
逐项积分得:
$\varphi_3(x) = \frac{1}{2}x^2 + \frac{1}{20}x^5 + \frac{1}{160}x^8 + \frac{1}{4400}x^{11}$