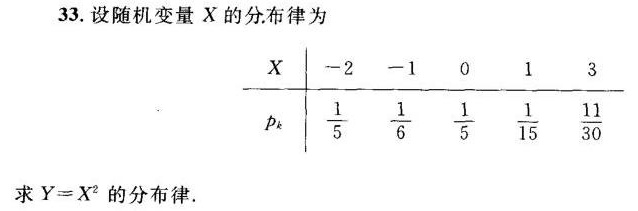
33.设随机变量X的分.布律为-|||-X -2 -1 0 1 3-|||-pk 1/5 1/6 1/5 1/15 11/30

考查要点：本题主要考查随机变量函数的分布律求解方法，即已知随机变量$X$的分布律，求$Y = X^2$的分布律。

解题核心思路：

1. 确定$Y$的可能取值：将$X$的每个取值代入$Y = X^2$，得到对应的$Y$值。
2. 合并相同$Y$值的概率：若不同的$X$取值对应相同的$Y$值，则将这些$X$取值对应的概率相加，得到该$Y$值的总概率。
3. 验证概率和为1：确保最终所有$Y$值的概率之和为1。

破题关键点：

• 正确计算平方后的$Y$值，注意符号的影响（如$X = -1$和$X = 1$均对应$Y = 1$）。
• 分类合并概率，避免遗漏或重复。

1. 确定$Y$的可能取值：

   • $X = -2 \Rightarrow Y = (-2)^2 = 4$
   • $X = -1 \Rightarrow Y = (-1)^2 = 1$
   • $X = 0 \Rightarrow Y = 0^2 = 0$
   • $X = 1 \Rightarrow Y = 1^2 = 1$
   • $X = 3 \Rightarrow Y = 3^2 = 9$
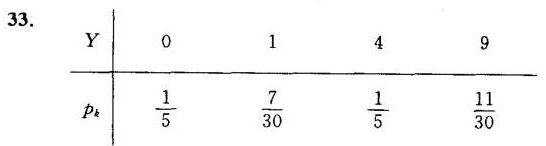
     因此，$Y$的可能取值为$0, 1, 4, 9$。

2. 计算各$Y$值的概率：

   • $Y = 0$：仅当$X = 0$时发生，概率为$p_X(0) = \dfrac{1}{5}$。
   • $Y = 1$：当$X = -1$或$X = 1$时发生，概率为：
     $p_Y(1) = p_X(-1) + p_X(1) = \dfrac{1}{6} + \dfrac{1}{15} = \dfrac{5}{30} + \dfrac{2}{30} = \dfrac{7}{30}$
   • $Y = 4$：仅当$X = -2$时发生，概率为$p_X(-2) = \dfrac{1}{5}$。
   • $Y = 9$：仅当$X = 3$时发生，概率为$p_X(3) = \dfrac{11}{30}$。

3. 验证概率和为1：
   $\dfrac{1}{5} + \dfrac{7}{30} + \dfrac{1}{5} + \dfrac{11}{30} = \dfrac{6}{30} + \dfrac{7}{30} + \dfrac{6}{30} + \dfrac{11}{30} = \dfrac{30}{30} = 1$
   验证通过。