2.利用极限存在的准则证明:-|||-(1) lim _(narrow infty )n(dfrac (1)({n)^2+pi }+dfrac (1)({n)^2+2pi }+... +dfrac (1)({n)^2+npi })= 1.
 .
.
题目解答
答案
证明:
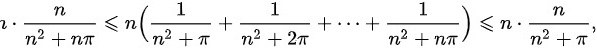
而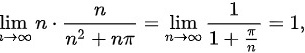
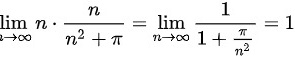
再由夹逼准则可得
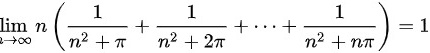
解析
考查要点:本题主要考查夹逼准则(夹挤定理)的应用,以及如何通过构造适当的不等式来求解数列极限。
解题核心思路:
- 观察和式的结构:和式中的每一项分母为 $n^2 + k\pi$($k$ 从 $1$ 到 $n$),整体乘以 $n$。
- 构造不等式:通过比较分母的大小关系,找到和式的上下界。
- 求极限:分别计算上下界的极限,若两者极限相同,则原式极限为此值。
破题关键点:
- 分母的大小关系:当 $k$ 增大时,分母 $n^2 + k\pi$ 增大,因此 $\frac{1}{n^2 + k\pi}$ 减小。
- 上下界的选择:利用最小分母和最大分母分别构造和式的上下界,进而得到整体表达式的上下限。
步骤1:构造不等式
分析分母的范围:
对于 $k = 1, 2, \dots, n$,分母满足
$n^2 + \pi \leq n^2 + k\pi \leq n^2 + n\pi.$
因此,每一项满足
$\frac{1}{n^2 + n\pi} \leq \frac{1}{n^2 + k\pi} \leq \frac{1}{n^2 + \pi}.$
求和并乘以 $n$:
将上述不等式对 $k$ 从 $1$ 到 $n$ 求和,得到
$n \cdot \frac{n}{n^2 + n\pi} \leq n \left( \sum_{k=1}^n \frac{1}{n^2 + k\pi} \right) \leq n \cdot \frac{n}{n^2 + \pi}.$
步骤2:计算上下限的极限
左边极限:
$\lim_{n \to \infty} \frac{n^2}{n^2 + n\pi} = \lim_{n \to \infty} \frac{1}{1 + \frac{\pi}{n}} = 1.$
右边极限:
$\lim_{n \to \infty} \frac{n^2}{n^2 + \pi} = \lim_{n \to \infty} \frac{1}{1 + \frac{\pi}{n^2}} = 1.$
步骤3:应用夹逼准则
由于上下限的极限均为 $1$,根据夹逼准则,原式极限为
$\lim_{n \to \infty} n \left( \sum_{k=1}^n \frac{1}{n^2 + k\pi} \right) = 1.$