题目
举反例说明下列命题是错误的:(1)若A²=0,则A=0;
举反例说明下列命题是错误的:
(1)若A²=0,则A=0;
题目解答
答案
不妨取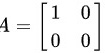 ,就有
,就有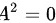 ,但
,但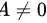
解析
考查要点:本题主要考查对命题“若$A^2=0$,则$A=0$”的理解,以及寻找反例的能力。关键在于认识到该命题在特定数学结构(如矩阵)中不成立。
解题核心思路:
- 明确命题的适用范围:若在实数范围内,命题成立;但需考虑更复杂的结构(如矩阵)。
- 构造非零矩阵:寻找一个非零矩阵$A$,使得$A^2=0$。
- 验证反例的有效性:确保$A \neq 0$且$A^2=0$。
破题关键点:
- 幂零矩阵的概念:存在非零矩阵满足$A^2=0$。
- 具体构造方法:利用简单上三角矩阵或分块矩阵构造反例。
第(1)题
反例构造:
取矩阵
$A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}$
验证:
- 计算$A^2$:
$A^2 = A \cdot A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 \cdot 0 + 1 \cdot 0 & 0 \cdot 1 + 1 \cdot 0 \\ 0 \cdot 0 + 0 \cdot 0 & 0 \cdot 1 + 0 \cdot 0 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$ - 验证$A \neq 0$:
矩阵$A$中存在元素$1$,因此$A$不是零矩阵。
结论:该矩阵满足$A^2=0$但$A \neq 0$,说明原命题不成立。