题目
设为球面下半部分的下侧，则正确的结论是（ ）( A ) ; ( B ) ; ( C ) ; ( D ) ;
设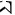
为球面
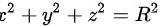下半部分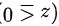
的下侧，则正确的结论是（ ）
( A )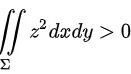 
;
( B )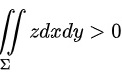 
;
( C )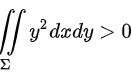 
;
( D )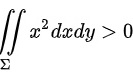 
;
题目解答
答案
依题知，
投影到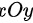
坐标面上是以原点为圆心，以
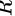为半径的圆，即
，
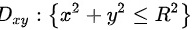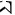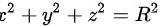且为球面下半部分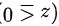的下侧，与球面法向量为锐角，
则：
对于A选项，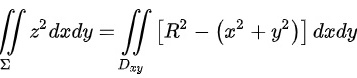
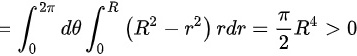，即A选项正确；
对于B选项，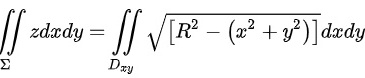
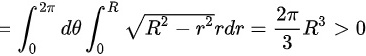，即B选项正确；
对于C选项，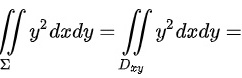
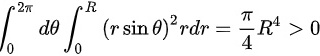，即C选项正确；
对于D选项，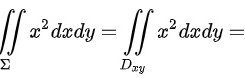
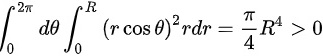，即D选项正确；
综上，本题选择A、B、C、D选项。
解析
步骤 1：确定投影区域
球面${x}^{2}+{y}^{2}+{z}^{2}={R}^{2}$下半部分$(z\leqslant 0)$的投影到$xy$坐标面上是以原点为圆心，$R$为半径的圆，即$D:y:\{ {x}^{2}+{y}^{2}\leqslant {R}^{2}\} $。
步骤 2：计算积分
对于A选项，${\int }_{{z}^{2}}dxdy=$ $\iint [ {R}^{2}-({x}^{2}+{y}^{2})] dxdy$$={\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}({R}^{2}-{r}^{2})rdr=\dfrac {\pi }{2}{R}^{4}\gt 0$，即A选项正确；
对于B选项，zdxdy= $\iint \sqrt {[ {R}^{2}-({x}^{2}+{y}^{2})] }dxdy$ ∑ Dxy$2\pi $ = $d.\theta $ $\sqrt {{R}^{2}-{r}^{2}}rdr=\dfrac {2\pi }{3}{R}^{3}\gt 0$，即B选项正确；
对于C选项，y^2dxdy= $\int {y}^{2}dxdy=$${\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}{(r\sin \theta )}^{2}rdr=\dfrac {\pi }{4}{R}^{4}\gt 0$，即C选项正确；
对于D选项，x^2dxdy= x^2dxdy= $D$${\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}{(r\cos \theta )}^{2}rdr=\dfrac {\pi }{4}{R}^{4}\gt 0$，即D选项正确；
步骤 3：总结
综上，本题选择A、B、C、D选项。
球面${x}^{2}+{y}^{2}+{z}^{2}={R}^{2}$下半部分$(z\leqslant 0)$的投影到$xy$坐标面上是以原点为圆心，$R$为半径的圆，即$D:y:\{ {x}^{2}+{y}^{2}\leqslant {R}^{2}\} $。
步骤 2：计算积分
对于A选项，${\int }_{{z}^{2}}dxdy=$ $\iint [ {R}^{2}-({x}^{2}+{y}^{2})] dxdy$$={\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}({R}^{2}-{r}^{2})rdr=\dfrac {\pi }{2}{R}^{4}\gt 0$，即A选项正确；
对于B选项，zdxdy= $\iint \sqrt {[ {R}^{2}-({x}^{2}+{y}^{2})] }dxdy$ ∑ Dxy$2\pi $ = $d.\theta $ $\sqrt {{R}^{2}-{r}^{2}}rdr=\dfrac {2\pi }{3}{R}^{3}\gt 0$，即B选项正确；
对于C选项，y^2dxdy= $\int {y}^{2}dxdy=$${\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}{(r\sin \theta )}^{2}rdr=\dfrac {\pi }{4}{R}^{4}\gt 0$，即C选项正确；
对于D选项，x^2dxdy= x^2dxdy= $D$${\int }_{0}^{2\pi }d\theta {\int }_{0}^{R}{(r\cos \theta )}^{2}rdr=\dfrac {\pi }{4}{R}^{4}\gt 0$，即D选项正确；
步骤 3：总结
综上，本题选择A、B、C、D选项。