题目
若连接两点(3,8,-5), B(1,12,z)的线段与平面(3,8,-5), B(1,12,z)平行则(3,8,-5), B(1,12,z)A 5 B -5 C -25 D 25
若连接两点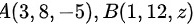
的线段与平面
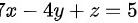平行则
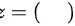
A 5
B -5
C -25
D 25
题目解答
答案
由题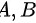
两点坐标可计算的向量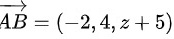
而平面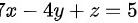的法向量为量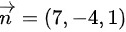
线段与平面平行，可得向量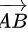
与法向量
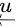垂直，
故有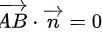
即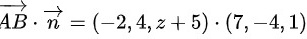
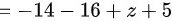
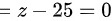
故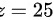
即本题答案为D。
解析
步骤 1：计算向量$\overrightarrow {AB}$
根据点A(3,8,-5)和点B(1,12,z)的坐标，可以计算向量$\overrightarrow {AB}$的坐标为：
$\overrightarrow {AB} = (1-3, 12-8, z+5) = (-2, 4, z+5)$
步骤 2：确定平面的法向量
平面7x-4y+z=5的法向量为$\overrightarrow {n}=(7,-4,1)$
步骤 3：利用向量垂直的条件
由于线段AB与平面平行，向量$\overrightarrow {AB}$与平面的法向量$\overrightarrow {n}$垂直，因此它们的点积为0，即：
$\overrightarrow {AB}\cdot \overrightarrow {n} = (-2, 4, z+5)\cdot (7,-4,1) = 0$
步骤 4：计算点积并求解z
计算点积：
$(-2)\cdot 7 + 4\cdot (-4) + (z+5)\cdot 1 = 0$
$-14 - 16 + z + 5 = 0$
$z - 25 = 0$
$z = 25$
根据点A(3,8,-5)和点B(1,12,z)的坐标，可以计算向量$\overrightarrow {AB}$的坐标为：
$\overrightarrow {AB} = (1-3, 12-8, z+5) = (-2, 4, z+5)$
步骤 2：确定平面的法向量
平面7x-4y+z=5的法向量为$\overrightarrow {n}=(7,-4,1)$
步骤 3：利用向量垂直的条件
由于线段AB与平面平行，向量$\overrightarrow {AB}$与平面的法向量$\overrightarrow {n}$垂直，因此它们的点积为0，即：
$\overrightarrow {AB}\cdot \overrightarrow {n} = (-2, 4, z+5)\cdot (7,-4,1) = 0$
步骤 4：计算点积并求解z
计算点积：
$(-2)\cdot 7 + 4\cdot (-4) + (z+5)\cdot 1 = 0$
$-14 - 16 + z + 5 = 0$
$z - 25 = 0$
$z = 25$