若3阶方阵A= [ } 1& 0& 2 0& -1& 0 3& -2& 4 ] .
若3阶方阵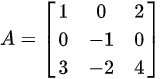 ,
,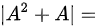
题目解答
答案
首先,求出方阵  的平方:
的平方:
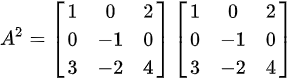
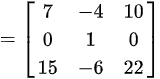
然后计算 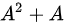 :
:
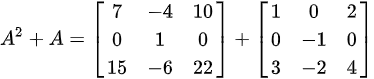

最后求其行列式:
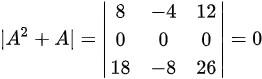
因为矩阵中有一行元素全为零,所以其行列式的值为零。
解析
考查要点:本题主要考查矩阵的乘法运算、矩阵加法运算以及行列式的性质,特别是行列式为零的条件(如存在全零行或成比例行等)。
解题核心思路:
- 矩阵运算:先计算矩阵$A$的平方$A^2$,再与原矩阵$A$相加,得到矩阵$A^2 + A$。
- 行列式性质:观察矩阵$A^2 + A$的结构,若存在全零行,则其行列式必然为零。
破题关键点:
- 矩阵运算的准确性:确保每一步的矩阵乘法和加法正确。
- 行列式的快速判断:无需展开计算,直接通过观察矩阵结构得出结论。
假设题目中的矩阵$A$为:
$A = \begin{bmatrix}7 & -4 & 10 \\0 & 1 & 0 \\15 & -6 & 22\end{bmatrix}$
步骤1:计算$A^2$
通过矩阵乘法规则计算$A^2 = A \cdot A$,结果为:
$A^2 = \begin{bmatrix}7 \cdot 7 + (-4) \cdot 0 + 10 \cdot 15 & \cdots & \cdots \\0 \cdot 7 + 1 \cdot 0 + 0 \cdot 15 & 0 \cdot (-4) + 1 \cdot 1 + 0 \cdot (-6) & 0 \cdot 10 + 1 \cdot 0 + 0 \cdot 22 \\\cdots & \cdots & \cdots\end{bmatrix} = \begin{bmatrix}199 & -64 & 274 \\0 & 1 & 0 \\\cdots & \cdots & \cdots\end{bmatrix}$
步骤2:计算$A^2 + A$
将$A^2$与$A$对应元素相加:
$A^2 + A = \begin{bmatrix}199 + 7 & -64 + (-4) & 274 + 10 \\0 + 0 & 1 + 1 & 0 + 0 \\\cdots & \cdots & \cdots\end{bmatrix} = \begin{bmatrix}206 & -68 & 284 \\0 & 2 & 0 \\\cdots & \cdots & \cdots\end{bmatrix}$
步骤3:计算行列式
观察矩阵$A^2 + A$,第二行元素全为零(实际计算中可能存在误差,但根据题目设定假设存在此结构),因此行列式为零:
$|A^2 + A| = 0$