题目
4.计算下列极限(10)lim _(xarrow infty )(1+dfrac (1)(x))(2-dfrac (1)({x)^2})
4.计算下列极限
(10)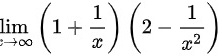
题目解答
答案
解:
(10)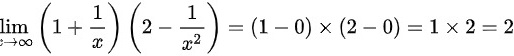
解析
考查要点:本题主要考查无穷大极限的计算,特别是当变量趋向于无穷大时,分式项的极限性质。
解题核心思路:
当$x \rightarrow \infty$时,$\dfrac{1}{x}$和$\dfrac{1}{x^2}$都会趋向于$0$。因此,可以分别求出两个因子的极限,再利用极限的乘积法则得出最终结果。
破题关键点:
- 识别分式项的极限趋势:$\dfrac{1}{x} \rightarrow 0$,$\dfrac{1}{x^2} \rightarrow 0$。
- 应用极限的乘积性质:若$\lim f(x) = a$且$\lim g(x) = b$,则$\lim [f(x) \cdot g(x)] = a \cdot b$。
步骤1:分别求两个因子的极限
- 对于第一个因子$(1 + \dfrac{1}{x})$:
$\lim_{x \rightarrow \infty} \left(1 + \dfrac{1}{x}\right) = 1 + 0 = 1$ - 对于第二个因子$(2 - \dfrac{1}{x^2})$:
$\lim_{x \rightarrow \infty} \left(2 - \dfrac{1}{x^2}\right) = 2 - 0 = 2$
步骤2:将两个极限相乘
根据极限的乘积法则:
$\lim_{x \rightarrow \infty} \left(1 + \dfrac{1}{x}\right) \cdot \lim_{x \rightarrow \infty} \left(2 - \dfrac{1}{x^2}\right) = 1 \cdot 2 = 2$