题目
将如图所示的DFA最小化。b b a-|||-1 a ③3) a-|||-4-|||-b 2-|||-a-|||-b bigcirc a
将如图所示的DFA最小化。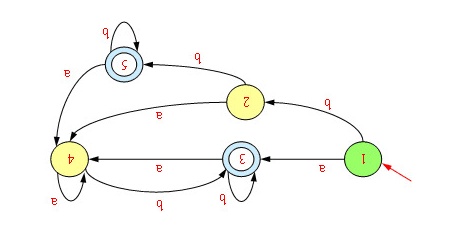
题目解答
答案
答: 现将DFA M最小化:
(ⅰ) 初始分划由两个子集组成,即:
π:{1,2,4}, {3,5}
(ⅱ) 为得到下一分划,考察子集{1,2,4}。因为
{1}a ={3}{3,5}
而 {2,4}a ={4}{1,2,4}
故1与2,4可区分,于是便得到下一分划:
π1: {1}, {2,4}, {3,5}
(ⅲ) 为得到下一分划,考察子集{3,5}。因为
{3}a ={5}a ={4}
又因为 {3}b ={3}{3,5}, {5}b ={5}{3,5}
故3和5等价,于是得到的下一分划与π1相同:
π2: {1}, {2,4}, {3,5}
(ⅳ) 再考察子集{2,4},因为
{2}a ={4}a ={4}
又因为 {2}b ={5}, {4}b ={3}, 且3与5等价,
故2和4等价,于是得到的下一分划与π2相同:
π3: {1}, {2,4}, {3,5}
此时子集已全部分裂,故最小化的过程宣告结束。
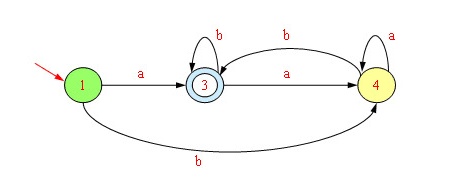
(ⅴ)现选择状态4作为{2,4}的代表,状态3作为{3,5}的代表,将状态2,5从状态转换图中删去,并将原来引至2的矢线都引至4,将原来引至5的矢线都引至3,这样,我们就得到了最小化后的DFA M′如下图所示。
解析
步骤 1:初始分划
初始分划由两个子集组成,即:
π: {1,2,4}, {3,5}
步骤 2:考察子集{1,2,4}
考察子集{1,2,4}。因为
{1}a = {3} ∈ {3,5}
而 {2,4}a = {4} ∈ {1,2,4}
故1与2,4可区分,于是便得到下一分划:
π1: {1}, {2,4}, {3,5}
步骤 3:考察子集{3,5}
为得到下一分划,考察子集{3,5}。因为
{3}a = {5}a = {4}
又因为 {3}b = {3} ∈ {3,5}, {5}b = {5} ∈ {3,5}
故3和5等价,于是得到的下一分划与π1相同:
π2: {1}, {2,4}, {3,5}
步骤 4:考察子集{2,4}
再考察子集{2,4},因为
{2}a = {4}a = {4}
又因为 {2}b = {5}, {4}b = {3}, 且3与5等价,
故2和4等价,于是得到的下一分划与π2相同:
π3: {1}, {2,4}, {3,5}
步骤 5:最小化过程结束
此时子集已全部分裂,故最小化的过程宣告结束。
步骤 6:选择状态代表
现选择状态4作为{2,4}的代表,状态3作为{3,5}的代表,将状态2,5从状态转换图中删去,并将原来引至2的矢线都引至4,将原来引至5的矢线都引至3,这样,我们就得到了最小化后的DFA M′如下图所示。
初始分划由两个子集组成,即:
π: {1,2,4}, {3,5}
步骤 2:考察子集{1,2,4}
考察子集{1,2,4}。因为
{1}a = {3} ∈ {3,5}
而 {2,4}a = {4} ∈ {1,2,4}
故1与2,4可区分,于是便得到下一分划:
π1: {1}, {2,4}, {3,5}
步骤 3:考察子集{3,5}
为得到下一分划,考察子集{3,5}。因为
{3}a = {5}a = {4}
又因为 {3}b = {3} ∈ {3,5}, {5}b = {5} ∈ {3,5}
故3和5等价,于是得到的下一分划与π1相同:
π2: {1}, {2,4}, {3,5}
步骤 4:考察子集{2,4}
再考察子集{2,4},因为
{2}a = {4}a = {4}
又因为 {2}b = {5}, {4}b = {3}, 且3与5等价,
故2和4等价,于是得到的下一分划与π2相同:
π3: {1}, {2,4}, {3,5}
步骤 5:最小化过程结束
此时子集已全部分裂,故最小化的过程宣告结束。
步骤 6:选择状态代表
现选择状态4作为{2,4}的代表,状态3作为{3,5}的代表,将状态2,5从状态转换图中删去,并将原来引至2的矢线都引至4,将原来引至5的矢线都引至3,这样,我们就得到了最小化后的DFA M′如下图所示。