题目
已知f(x)是可导的函数,则f(x)( )A. ,f(x); B. ,f(x); C. ,f(x); D. ,f(x)
已知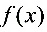 是可导的函数,则
是可导的函数,则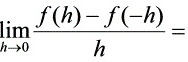 ( )
( )
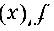 ;
;B. ,
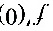 ;
;C. ,
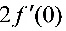 ;
;D. ,
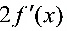
题目解答
答案
C. $2f'(0)$
解析
考查要点:本题主要考查导数的定义及极限的计算,需要学生理解导数的本质,并能灵活运用导数的定义式进行变形。
解题核心思路:
题目中的极限形式与导数的定义式相似,但分子为$f(h)-f(-h)$,需通过变形将其转化为已知点(通常是$x=0$)的导数表达式。关键在于将分子拆分为两个导数的组合,或利用洛必达法则直接求解。
破题关键点:
- 识别导数定义的变形:分子中的$f(h)-f(-h)$可拆解为$f(h)-f(0)$和$f(0)-f(-h)$两部分,分别对应$f'(0)$的定义式。
- 灵活应用导数性质:若分子分母均趋近于0,可考虑使用洛必达法则简化计算。
方法一:拆分分子
将分子$f(h)-f(-h)$拆分为两部分:
$\begin{aligned}\lim_{h \to 0} \frac{f(h)-f(-h)}{h} &= \lim_{h \to 0} \left( \frac{f(h)-f(0)}{h} + \frac{f(0)-f(-h)}{h} \right) \\&= \lim_{h \to 0} \frac{f(h)-f(0)}{h} + \lim_{h \to 0} \frac{f(0)-f(-h)}{h}.\end{aligned}$
- 第一项$\lim_{h \to 0} \frac{f(h)-f(0)}{h}$是$f'(0)$的定义式。
- 第二项中,令$k = -h$,则当$h \to 0$时$k \to 0$,原式变为:
$\lim_{k \to 0} \frac{f(0)-f(k)}{-k} = \lim_{k \to 0} \frac{f(k)-f(0)}{k} = f'(0).$
因此,原式等于$f'(0) + f'(0) = 2f'(0)$。
方法二:洛必达法则
分子$f(h)-f(-h)$和分母$h$在$h \to 0$时均趋近于0,满足洛必达法则条件:
$\begin{aligned}\lim_{h \to 0} \frac{f(h)-f(-h)}{h} &= \lim_{h \to 0} \frac{f'(h) + f'(-h)}{1} \quad (\text{对分子分母分别求导}) \\&= f'(0) + f'(0) = 2f'(0).\end{aligned}$