(8)lim ((sin x))^tan x-|||-arrow dfrac (pi )(2)
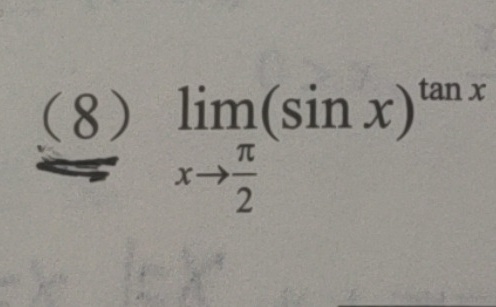
题目解答
答案

解析
本题考查重要极限、等价无穷小替换以及洛必达法则在求解极限中的应用,核心是处理$1^\infty$型极限问题。
步骤1:识别极限类型
当$x\rightarrow\frac{\pi}{2}$时:
- $\sin x\rightarrow\sin\frac{\pi}{2}=1$
- $\tan x\rightarrow\tan\frac{\pi}{2}\rightarrow+\infty$
故原式为$1^\infty$型极限,需转化为指数形式求解。
步骤2:转化为指数形式
对$(\sin x)^{\tan x}$取自然对数,设$L=\lim_{x\rightarrow\frac{\pi}{2}}(\sin x)^{\tan x}$,则:
$\ln L=\lim_{x\rightarrow\frac{\pi}{2}}\ln\left[(\sin x)^{\tan x}\right]=\lim_{x\rightarrow\frac{\pi}{2}}\tan x\cdot\ln\sin x$
此时$\tan x\rightarrow+\infty$,$\ln\sin x\rightarrow\ln1=0$,转化为$\infty\cdot0$型极限,进一步改写为$\frac{0}{0}$型以便用洛必达法则:
$\ln L=\lim_{x\rightarrow\frac{\pi}{2}}\frac{\ln\sin x}{\cot x}\quad(\text{因}\cot x=\frac{1}{\tan x}\rightarrow0)$
步骤3:应用洛必达法则
对分子分母分别求导:
- 分子导数:$(\ln\sin x)'=\frac{\cos x}{\sin x}=\cot x$
- 分母导数:$(\cot x)'=-\csc^2 x=-\frac{1}{\sin^2 x}$
代入得:
$\ln L=\lim_{x\rightarrow\frac{\pi}{2}}\frac{\cot x}{-\frac{1}{\sin^2 x}}=\lim_{x\rightarrow\frac{\pi}{2}}-\cot x\cdot\sin^2 x$
化简$\cot x\cdot\sin^2 x=\frac{\cos x}{\sin x}\cdot\sin^2 x=\sin x\cos x$,故:
$\ln L=\lim_{x\rightarrow\frac{\pi}{2}}(-\sin x\cos x)=-\sin\frac{\pi}{2}\cos\frac{\pi}{2}=-1\cdot0=0$
步骤4:还原指数形式
因$\ln L=0$,故$L=e^0=1$。