题目
求微分方程sqrt (x)y'=(y)^2+1的通解。
求微分方程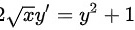 的通解。
的通解。
题目解答
答案
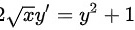
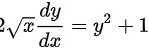
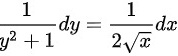
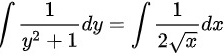
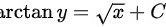
所以通解为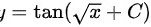 ,
,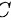 为常数。
为常数。
解析
考查要点:本题主要考查可分离变量微分方程的解法,需要将方程中的变量分离后分别积分。
解题核心思路:
- 变量分离:将方程整理为关于$y$的函数和关于$x$的函数分别位于等式两边。
- 积分求解:对两边分别积分,注意积分常数的处理。
- 解显式表达:将积分结果整理为关于$y$的显式表达式。
破题关键点:
- 识别方程类型为可分离变量方程。
- 正确分离变量并积分,特别是左边$\int \frac{1}{y^2+1} dy$对应反正切函数,右边$\int \frac{1}{2\sqrt{x}} dx$需用幂函数积分公式。
步骤1:变量分离
原方程:
$2\sqrt{x} y' = y^2 + 1$
将$y'$表示为$\frac{dy}{dx}$,并整理得:
$\frac{1}{y^2 + 1} dy = \frac{1}{2\sqrt{x}} dx$
步骤2:两边积分
对左边积分:
$\int \frac{1}{y^2 + 1} dy = \arctan y + C_1$
对右边积分:
$\int \frac{1}{2\sqrt{x}} dx = \int \frac{1}{2} x^{-1/2} dx = \frac{1}{2} \cdot 2x^{1/2} + C_2 = \sqrt{x} + C_2$
步骤3:合并常数并整理
联立积分结果,合并常数项:
$\arctan y = \sqrt{x} + C$
其中$C = C_2 - C_1$为任意常数。
步骤4:解显式表达
取正切函数得通解:
$y = \tan(\sqrt{x} + C)$