题目
计算d/dxy-1xln(1+x^2) dx=（）
计算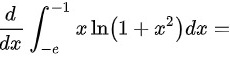
（）
题目解答
答案
对于定积分
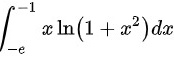
其值一定为常数
设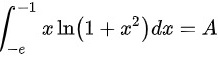
∴原式
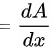
常数对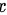
的导数值均为零
即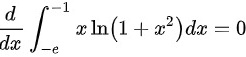
即本题答案为
解析
步骤 1：理解定积分的性质
定积分${\int }_{-e}^{-1}x\ln (1+{x}^{2})dx$表示的是函数$f(x)=x\ln (1+{x}^{2})$在区间$[-e, -1]$上的积分值。由于积分区间是固定的，因此该定积分的值是一个常数，记为$A$。
步骤 2：求导数
根据导数的定义，求导数$\dfrac {d}{dx}{\int }_{-e}^{-1}x\ln (1+{x}^{2})dx$等价于求导数$\dfrac {dA}{dx}$。由于$A$是一个常数，常数的导数为零。
步骤 3：得出结论
因此，$\dfrac {d}{dx}{\int }_{-e}^{-1}x\ln (1+{x}^{2})dx=0$。
定积分${\int }_{-e}^{-1}x\ln (1+{x}^{2})dx$表示的是函数$f(x)=x\ln (1+{x}^{2})$在区间$[-e, -1]$上的积分值。由于积分区间是固定的，因此该定积分的值是一个常数，记为$A$。
步骤 2：求导数
根据导数的定义，求导数$\dfrac {d}{dx}{\int }_{-e}^{-1}x\ln (1+{x}^{2})dx$等价于求导数$\dfrac {dA}{dx}$。由于$A$是一个常数，常数的导数为零。
步骤 3：得出结论
因此，$\dfrac {d}{dx}{\int }_{-e}^{-1}x\ln (1+{x}^{2})dx=0$。