题目
3.6 计算 (int )_(c)dfrac (1)({z)^2-z}dz, 其中C为圆周 |z|=2.
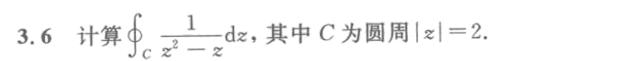
题目解答
答案
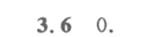
解析
考查要点:本题主要考查复变函数中的围道积分计算,特别是利用留数定理求解积分的方法。
解题核心思路:
- 分解被积函数,确定积分路径内的奇点位置;
- 计算各奇点的留数;
- 应用留数定理,将积分转化为留数之和的计算。
破题关键点:
- 正确分解分母:将被积函数 $\frac{1}{z^2 - z}$ 分解为 $\frac{1}{z(z-1)}$,找到奇点 $z=0$ 和 $z=1$;
- 判断奇点是否在积分路径内:圆周 $|z|=2$ 的半径为 $2$,两个奇点均在路径内部;
- 计算一阶极点的留数:分别计算 $z=0$ 和 $z=1$ 处的留数并求和。
步骤1:分解被积函数
将被积函数分解为部分分式:
$\frac{1}{z^2 - z} = \frac{1}{z(z-1)}.$
此时,被积函数的奇点为 $z=0$ 和 $z=1$,均为一阶极点。
步骤2:判断奇点位置
积分路径为圆周 $|z|=2$,半径 $2$ 大于 $|0|=0$ 和 $|1|=1$,因此两个奇点均在路径内部。
步骤3:计算留数
- 在 $z=0$ 处:
根据一阶极点留数公式:
$\text{Res}(f, 0) = \lim_{z \to 0} z \cdot \frac{1}{z(z-1)} = \lim_{z \to 0} \frac{1}{z-1} = -1.$ - 在 $z=1$ 处:
同理,
$\text{Res}(f, 1) = \lim_{z \to 1} (z-1) \cdot \frac{1}{z(z-1)} = \lim_{z \to 1} \frac{1}{z} = 1.$
步骤4:应用留数定理
积分结果为 $2\pi i$ 乘以留数之和:
$\int_C \frac{1}{z^2 - z} \, dz = 2\pi i \cdot (\text{Res}(f, 0) + \text{Res}(f, 1)) = 2\pi i \cdot (-1 + 1) = 0.$