题目
设随机变量X的概率密度为(x)=A(e)^-|x|,(x)=A(e)^-|x|,则常数(x)=A(e)^-|x|,(x)=A(e)^-|x|.A.(x)=A(e)^-|x|,(x)=A(e)^-|x|B.(x)=A(e)^-|x|,(x)=A(e)^-|x|C.(x)=A(e)^-|x|,(x)=A(e)^-|x|D.(x)=A(e)^-|x|,(x)=A(e)^-|x|
设随机变量X的概率密度为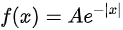 ,
,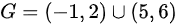 ,则常数
,则常数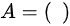 ,
,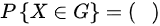 .
.
A.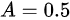 ,
,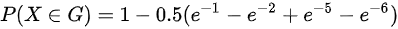
B.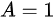 ,
,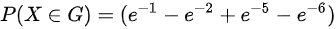
C.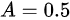 ,
,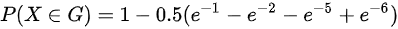
D.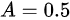 ,
,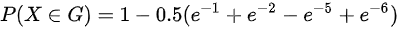
题目解答
答案
一维连续型随机变量概率密度函数的归一性,即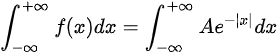
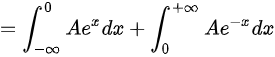
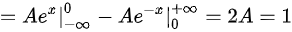 ,则
,则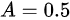 ,则
,则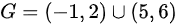 ,则常数
,则常数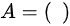 ,
,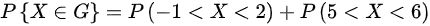
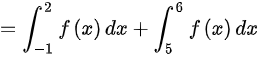
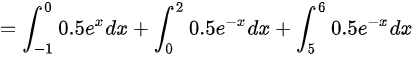
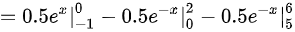
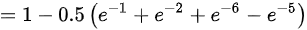 ,因此选择D。
,因此选择D。
解析
步骤 1:确定常数A
根据概率密度函数的归一性,即$f(x)dx=1$,我们有
$$
\int_{-\infty}^{+\infty} A e^{-|x|} dx = 1
$$
由于$e^{-|x|}$在$x<0$和$x>0$时有不同的形式,我们可以将积分分为两部分:
$$
\int_{-\infty}^{0} A e^{x} dx + \int_{0}^{+\infty} A e^{-x} dx = 1
$$
计算这两个积分,我们得到:
$$
A \int_{-\infty}^{0} e^{x} dx + A \int_{0}^{+\infty} e^{-x} dx = A \left[ e^{x} \right]_{-\infty}^{0} + A \left[ -e^{-x} \right]_{0}^{+\infty} = A(1) + A(1) = 2A = 1
$$
因此,$A = 0.5$。
步骤 2:计算$P\{ X\in G\}$
$G=(-1,2)\cup (5,6)$,则$P\{ X\in G\} = P(-1\lt X\lt 2)+P(5\lt X\lt 6)$
$$
P\{ X\in G\} = \int_{-1}^{2} 0.5 e^{-|x|} dx + \int_{5}^{6} 0.5 e^{-|x|} dx
$$
由于$-1\lt x\lt 2$时,$|x|=x$,$5\lt x\lt 6$时,$|x|=x$,我们有:
$$
P\{ X\in G\} = 0.5 \int_{-1}^{2} e^{-x} dx + 0.5 \int_{5}^{6} e^{-x} dx
$$
计算这两个积分,我们得到:
$$
P\{ X\in G\} = 0.5 \left[ -e^{-x} \right]_{-1}^{2} + 0.5 \left[ -e^{-x} \right]_{5}^{6} = 0.5 \left( -e^{-2} + e^{1} \right) + 0.5 \left( -e^{-6} + e^{-5} \right)
$$
$$
P\{ X\in G\} = 0.5 \left( e^{-1} - e^{-2} - e^{-6} + e^{-5} \right)
$$
因此,$P\{ X\in G\} = 1 - 0.5 \left( e^{-1} + e^{-2} - e^{-5} + e^{-6} \right)$。
根据概率密度函数的归一性,即$f(x)dx=1$,我们有
$$
\int_{-\infty}^{+\infty} A e^{-|x|} dx = 1
$$
由于$e^{-|x|}$在$x<0$和$x>0$时有不同的形式,我们可以将积分分为两部分:
$$
\int_{-\infty}^{0} A e^{x} dx + \int_{0}^{+\infty} A e^{-x} dx = 1
$$
计算这两个积分,我们得到:
$$
A \int_{-\infty}^{0} e^{x} dx + A \int_{0}^{+\infty} e^{-x} dx = A \left[ e^{x} \right]_{-\infty}^{0} + A \left[ -e^{-x} \right]_{0}^{+\infty} = A(1) + A(1) = 2A = 1
$$
因此,$A = 0.5$。
步骤 2:计算$P\{ X\in G\}$
$G=(-1,2)\cup (5,6)$,则$P\{ X\in G\} = P(-1\lt X\lt 2)+P(5\lt X\lt 6)$
$$
P\{ X\in G\} = \int_{-1}^{2} 0.5 e^{-|x|} dx + \int_{5}^{6} 0.5 e^{-|x|} dx
$$
由于$-1\lt x\lt 2$时,$|x|=x$,$5\lt x\lt 6$时,$|x|=x$,我们有:
$$
P\{ X\in G\} = 0.5 \int_{-1}^{2} e^{-x} dx + 0.5 \int_{5}^{6} e^{-x} dx
$$
计算这两个积分,我们得到:
$$
P\{ X\in G\} = 0.5 \left[ -e^{-x} \right]_{-1}^{2} + 0.5 \left[ -e^{-x} \right]_{5}^{6} = 0.5 \left( -e^{-2} + e^{1} \right) + 0.5 \left( -e^{-6} + e^{-5} \right)
$$
$$
P\{ X\in G\} = 0.5 \left( e^{-1} - e^{-2} - e^{-6} + e^{-5} \right)
$$
因此,$P\{ X\in G\} = 1 - 0.5 \left( e^{-1} + e^{-2} - e^{-5} + e^{-6} \right)$。