题目
下列关于无穷小的说法正确的是( )A 无穷小是一个很小的数B 无穷小是一个负数C 无穷小是0D 无穷小是极限为零的变量
下列关于无穷小的说法正确的是( )
A 无穷小是一个很小的数
B 无穷小是一个负数
C 无穷小是0
D 无穷小是极限为零的变量
题目解答
答案
由无穷小定义可知,无穷小即以数0为极限的变量,无限接近于0,当自变量x无限接近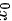 (或x的绝对值无限增大)时,函数值f(x)与0无限接近,即
(或x的绝对值无限增大)时,函数值f(x)与0无限接近,即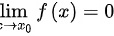 或
或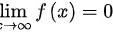 ,则称f(x)为当
,则称f(x)为当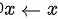 (或
(或 )时的无穷小量,故可知无穷小是极限为零的变量,故D对,A、B、C错.
)时的无穷小量,故可知无穷小是极限为零的变量,故D对,A、B、C错.
故答案为:D
解析
考查要点:本题主要考查对无穷小概念的理解,需要明确区分“无穷小”与“很小的数”“0”等概念的本质区别。
解题核心思路:
- 无穷小是变量,而非具体的数值;
- 无穷小的本质是极限为0,与自变量的变化过程相关;
- 排除混淆项时需注意:无穷小可以是正数、负数或任意符号,但最终必须满足极限为0的条件。
破题关键点:
- 明确无穷小的定义:以0为极限的变量;
- 识别选项中将变量与固定数值(如“很小的数”“0”)混淆的错误描述。
选项分析:
-
A选项:“无穷小是一个很小的数”
错误。无穷小是变量,其大小取决于自变量的变化过程,不能简单视为“很小的数”。例如,当$x \to 0$时,$x$是无穷小,但$x=0.1$时并不是无穷小。 -
B选项:“无穷小是一个负数”
错误。无穷小的符号可以任意,例如$\lim_{x \to 0} x = 0$(正数),$\lim_{x \to 0} (-x) = 0$(负数),但它们都属于无穷小。 -
C选项:“无穷小是0”
错误。0是确定的数,而无穷小是变量,其极限为0,但本身不等于0。例如,$\lim_{x \to \infty} \frac{1}{x} = 0$,但$\frac{1}{x}$本身是无穷小,而非0。 -
D选项:“无穷小是极限为零的变量”
正确。根据定义,若变量$f(x)$在自变量变化过程中满足$\lim f(x) = 0$,则称$f(x)$是该过程中的无穷小。