题目
将根式化为指数形式dfrac ({x)^2sqrt (x)}(sqrt [3]{x)}=
将根式化为指数形式
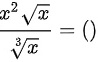
题目解答
答案
∵根值为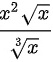
转化为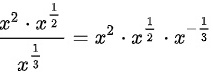
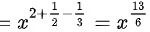
所以本题答案为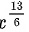
解析
步骤 1:将根式转化为指数形式
将根式 $\sqrt{x}$ 和 $\sqrt[3]{x}$ 转化为指数形式,即 $\sqrt{x} = x^{\frac{1}{2}}$ 和 $\sqrt[3]{x} = x^{\frac{1}{3}}$。
步骤 2:将原式转化为指数形式
将原式 $\dfrac{{x}^{2}\sqrt{x}}{\sqrt[3]{x}}$ 转化为指数形式,即 $\dfrac{{x}^{2}\cdot{x}^{\frac{1}{2}}}{{x}^{\frac{1}{3}}}$。
步骤 3:化简指数形式
根据指数法则,将指数形式化简,即 ${x}^{2}\cdot{x}^{\frac{1}{2}}\cdot{x}^{-\frac{1}{3}} = {x}^{2+\frac{1}{2}-\frac{1}{3}}$。
步骤 4:计算指数
计算指数 $2+\frac{1}{2}-\frac{1}{3}$,即 $2+\frac{1}{2}-\frac{1}{3} = \frac{13}{6}$。
将根式 $\sqrt{x}$ 和 $\sqrt[3]{x}$ 转化为指数形式,即 $\sqrt{x} = x^{\frac{1}{2}}$ 和 $\sqrt[3]{x} = x^{\frac{1}{3}}$。
步骤 2:将原式转化为指数形式
将原式 $\dfrac{{x}^{2}\sqrt{x}}{\sqrt[3]{x}}$ 转化为指数形式,即 $\dfrac{{x}^{2}\cdot{x}^{\frac{1}{2}}}{{x}^{\frac{1}{3}}}$。
步骤 3:化简指数形式
根据指数法则,将指数形式化简,即 ${x}^{2}\cdot{x}^{\frac{1}{2}}\cdot{x}^{-\frac{1}{3}} = {x}^{2+\frac{1}{2}-\frac{1}{3}}$。
步骤 4:计算指数
计算指数 $2+\frac{1}{2}-\frac{1}{3}$,即 $2+\frac{1}{2}-\frac{1}{3} = \frac{13}{6}$。