题目
10.对应二次型 ({x)_(1)}^2+4(x)_(1)(x)_(2)+3({x)_(2)}^2 的矩阵为 () .-|||-A. (} 1& -1 -1& 3 ) .
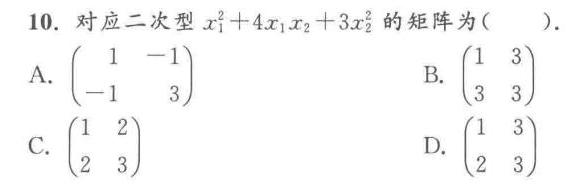
题目解答
答案
解析
步骤 1:二次型的矩阵表示
二次型 ${{x}_{1}}^{2}+4{x}_{1}{x}_{2}+3{{x}_{2}}^{2}$ 可以表示为 $x^{T}Ax$ 的形式,其中 $x = \left (\begin{matrix} x_{1}\\ x_{2}\end{matrix} ) \right.$,$A$ 是一个对称矩阵。
步骤 2:确定矩阵 $A$
根据二次型的系数,我们可以确定矩阵 $A$ 的元素。对于 ${{x}_{1}}^{2}$,系数为 1,对应矩阵 $A$ 的 $(1,1)$ 位置;对于 $4{x}_{1}{x}_{2}$,系数为 4,对应矩阵 $A$ 的 $(1,2)$ 和 $(2,1)$ 位置(因为矩阵是对称的);对于 $3{{x}_{2}}^{2}$,系数为 3,对应矩阵 $A$ 的 $(2,2)$ 位置。
步骤 3:写出矩阵 $A$
根据上述分析,矩阵 $A$ 为 $\left (\begin{matrix} 1& 2\\ 2& 3\end{matrix} ) \right.$。
二次型 ${{x}_{1}}^{2}+4{x}_{1}{x}_{2}+3{{x}_{2}}^{2}$ 可以表示为 $x^{T}Ax$ 的形式,其中 $x = \left (\begin{matrix} x_{1}\\ x_{2}\end{matrix} ) \right.$,$A$ 是一个对称矩阵。
步骤 2:确定矩阵 $A$
根据二次型的系数,我们可以确定矩阵 $A$ 的元素。对于 ${{x}_{1}}^{2}$,系数为 1,对应矩阵 $A$ 的 $(1,1)$ 位置;对于 $4{x}_{1}{x}_{2}$,系数为 4,对应矩阵 $A$ 的 $(1,2)$ 和 $(2,1)$ 位置(因为矩阵是对称的);对于 $3{{x}_{2}}^{2}$,系数为 3,对应矩阵 $A$ 的 $(2,2)$ 位置。
步骤 3:写出矩阵 $A$
根据上述分析,矩阵 $A$ 为 $\left (\begin{matrix} 1& 2\\ 2& 3\end{matrix} ) \right.$。