[题目]求值 lim _(narrow infty )(sqrt (n+1)-sqrt (n))

考查要点：本题主要考查数列极限的计算方法，特别是处理根号相减形式的极限问题。关键在于通过有理化消除根号，将原式转化为易于分析的形式。

解题核心思路：
当遇到形如$\sqrt{n+a} - \sqrt{n}$的表达式时，通常通过分子分母同乘共轭（即$\sqrt{n+a} + \sqrt{n}$）来有理化，从而简化表达式。此时分子会化简为常数，分母则为两个根号之和，随着$n$趋向无穷大，分母趋向无穷大，整体趋向0。

破题关键点：

1. 有理化：通过乘以共轭消除根号差。
2. 极限分析：明确分母$\sqrt{n+1} + \sqrt{n}$在$n \to \infty$时趋向无穷大。

步骤1：有理化处理
将原式分子分母同乘以$\sqrt{n+1} + \sqrt{n}$：
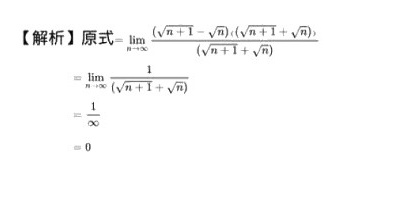
$\begin{aligned}\lim _{n\rightarrow \infty }(\sqrt {n+1}-\sqrt {n}) &= \lim _{n\rightarrow \infty } \frac{(\sqrt{n+1} - \sqrt{n})(\sqrt{n+1} + \sqrt{n})}{\sqrt{n+1} + \sqrt{n}} \\&= \lim _{n\rightarrow \infty } \frac{(n+1) - n}{\sqrt{n+1} + \sqrt{n}} \\&= \lim _{n\rightarrow \infty } \frac{1}{\sqrt{n+1} + \sqrt{n}}.\end{aligned}$

步骤2：分析分母趋势
当$n \to \infty$时，$\sqrt{n+1} \approx \sqrt{n}$，因此分母$\sqrt{n+1} + \sqrt{n} \approx 2\sqrt{n}$，显然趋向于无穷大。
故分式$\frac{1}{\sqrt{n+1} + \sqrt{n}}$趋向于$0$。

结论：
$\lim _{n\rightarrow \infty }(\sqrt {n+1}-\sqrt {n}) = 0.$