(int )_(0)^dfrac (pi {2)}sqrt (1-sin 2x)dx;
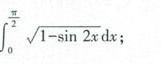
题目解答
答案

解析
考查要点:本题主要考查定积分的计算,特别是涉及绝对值函数的积分处理。关键在于将根号内的表达式转化为平方形式,从而简化被积函数,并根据积分区间内函数的正负性分段处理。
解题思路:
- 化简被积函数:利用三角恒等式,将根号内的表达式$1 - \sin 2x$写成$(\sin x - \cos x)^2$,从而$\sqrt{1 - \sin 2x} = |\sin x - \cos x|$。
- 分段处理绝对值:确定$\sin x - \cos x$的符号变化点$x = \frac{\pi}{4}$,将积分区间分为$[0, \frac{\pi}{4}]$和$[\frac{\pi}{4}, \frac{\pi}{2}]$,分别去掉绝对值符号。
- 分段积分求和:对两段区间分别积分,再将结果相加。
步骤1:化简被积函数
利用三角恒等式:
$1 - \sin 2x = (\sin x - \cos x)^2$
因此:
$\sqrt{1 - \sin 2x} = |\sin x - \cos x|$
步骤2:确定绝对值符号的分段点
解方程$\sin x - \cos x = 0$,得$x = \frac{\pi}{4}$。在区间$[0, \frac{\pi}{4}]$,$\cos x > \sin x$,故$|\sin x - \cos x| = \cos x - \sin x$;在区间$[\frac{\pi}{4}, \frac{\pi}{2}]$,$\sin x > \cos x$,故$|\sin x - \cos x| = \sin x - \cos x$。
步骤3:分段积分
-
第一段积分($0$到$\frac{\pi}{4}$):
$\int_{0}^{\frac{\pi}{4}} (\cos x - \sin x) \, dx = \left[ \sin x + \cos x \right]_{0}^{\frac{\pi}{4}} = \left( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \right) - (0 + 1) = \sqrt{2} - 1$ -
第二段积分($\frac{\pi}{4}$到$\frac{\pi}{2}$):
$\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (\sin x - \cos x) \, dx = \left[ -\cos x - \sin x \right]_{\frac{\pi}{4}}^{\frac{\pi}{2}} = \left( -0 - 1 \right) - \left( -\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \right) = \sqrt{2} - 1$
步骤4:求和
两段积分结果相加:
$(\sqrt{2} - 1) + (\sqrt{2} - 1) = 2\sqrt{2} - 2$