题目
在传染病流行期间设 t 为传染病开始流行的天数，人们被传染患病的速度可以近似地表示为=1000t(e)^-0.5t ，（r 的单位人 / 天 ) ，则传染病流行10天时累计患病人数 ( 从=1000t(e)^-0.5t开始计算 ) ，可用定积分表示为（）。A.=1000t(e)^-0.5t B.=1000t(e)^-0.5t C.=1000t(e)^-0.5t D.=1000t(e)^-0.5t
在传染病流行期间设 t 为传染病开始流行的天数，人们被传染患病的速度可以近似地表示为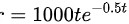
，（r 的单位人 / 天 ) ，则传染病流行10天时累计患病人数 ( 从
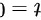开始计算 ) ，可用定积分表示为（）。
A.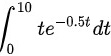
B.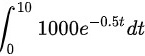
C.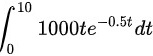
D.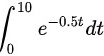
题目解答
答案
分析题意，人们被传染患病的速度可以近似地表示为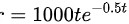 ，（r 的单位人 / 天 ) ，所以被积函数是 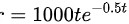，积分区间为从0到10，也就是说，传染病流行10天时累计患病人数 ( 从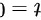开始计算 ) ，可用定积分表示为 。
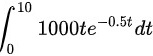故本题的答案为C。
解析
步骤 1：理解问题背景
题目描述了传染病流行期间，人们被传染患病的速度可以近似地表示为$=1000t{e}^{-0.5t}$，其中r的单位是人/天。我们需要计算传染病流行10天时累计患病人数。
步骤 2：确定被积函数和积分区间
根据题目描述，被传染患病的速度函数为$=1000t{e}^{-0.5t}$，因此被积函数就是这个函数。积分区间是从0到10天，因为我们要计算的是从开始流行到10天时的累计患病人数。
步骤 3：写出定积分表达式
根据步骤2，我们可以写出定积分表达式为${\int }_{0}^{10}1000t{e}^{-0.5t}dt$，这表示从0到10天内，每天被传染患病人数的总和。
题目描述了传染病流行期间，人们被传染患病的速度可以近似地表示为$=1000t{e}^{-0.5t}$，其中r的单位是人/天。我们需要计算传染病流行10天时累计患病人数。
步骤 2：确定被积函数和积分区间
根据题目描述，被传染患病的速度函数为$=1000t{e}^{-0.5t}$，因此被积函数就是这个函数。积分区间是从0到10天，因为我们要计算的是从开始流行到10天时的累计患病人数。
步骤 3：写出定积分表达式
根据步骤2，我们可以写出定积分表达式为${\int }_{0}^{10}1000t{e}^{-0.5t}dt$，这表示从0到10天内，每天被传染患病人数的总和。