题目
4.设随机变量X服从二项分布B(2,p),随机变量Y服从二项分布B(4,p).若-|||-. Xgeqslant 1 =dfrac (8)(9) ,试求 (Ygeqslant 1) -
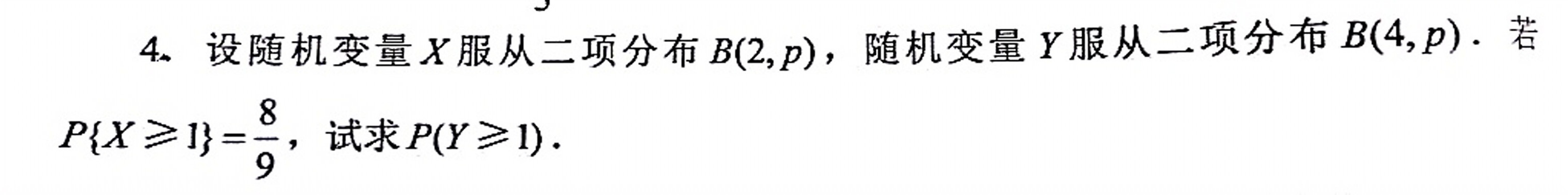
题目解答
答案

解析
考查要点:本题主要考查二项分布的概率计算,以及利用补集思想求解概率问题。
解题核心思路:
- 利用补集简化计算:对于“至少一个成功”的概率,转化为计算“全部不成功”的补集。
- 建立方程求参数:通过已知条件建立关于参数$p$的方程,解出$p$的值。
- 代入参数求目标概率:将求得的$p$代入目标分布,计算所求概率。
破题关键点:
- 二项分布公式:$P(X=k) = C(n,k)p^k(1-p)^{n-k}$。
- 补集思想:$P(X \geq 1) = 1 - P(X=0)$。
步骤1:求参数$p$
-
根据题意列方程:
已知$X \sim B(2,p)$,且$P(X \geq 1) = \dfrac{8}{9}$,则
$P(X \geq 1) = 1 - P(X=0) = \dfrac{8}{9}.$
因此,
$P(X=0) = 1 - \dfrac{8}{9} = \dfrac{1}{9}.$ -
代入二项分布公式:
$X=0$的概率为
$P(X=0) = C(2,0)p^0(1-p)^2 = (1-p)^2.$
由此得方程:
$(1-p)^2 = \dfrac{1}{9}.$ -
解方程求$p$:
解得
$1-p = \dfrac{1}{3} \quad (\text{舍去负根}),$
因此
$p = \dfrac{2}{3}.$
步骤2:求$P(Y \geq 1)$
-
计算$Y=0$的概率:
$Y \sim B(4,p)$,则
$P(Y=0) = C(4,0)p^0(1-p)^4 = (1-p)^4.$
代入$p = \dfrac{2}{3}$,得
$P(Y=0) = \left(1 - \dfrac{2}{3}\right)^4 = \left(\dfrac{1}{3}\right)^4 = \dfrac{1}{81}.$ -
利用补集求结果:
$P(Y \geq 1) = 1 - P(Y=0) = 1 - \dfrac{1}{81} = \dfrac{80}{81}.$