题目
8.设函数 f(x)= ) (x)^2+1,-xleqslant xlt 0 x+2,0leqslant xleqslant pi . 的傅里叶级数的和函数为S(x),-|||-则 (O)= __
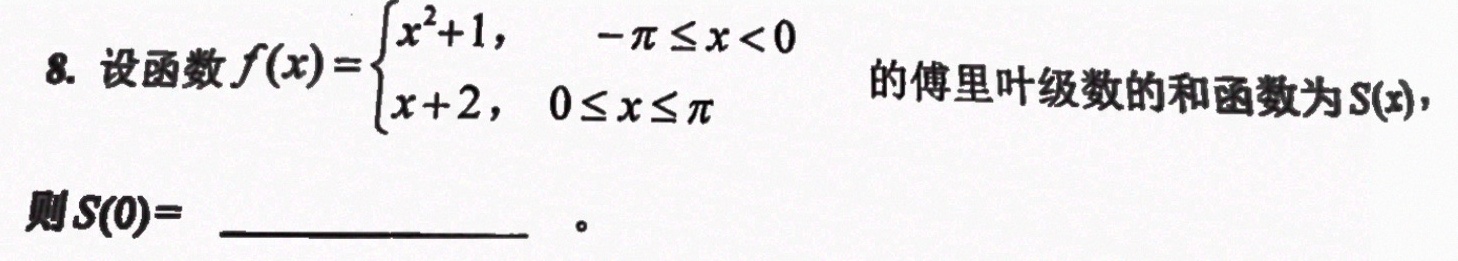
题目解答
答案

解析
步骤 1:确定函数在 x=0 处的左极限和右极限
- 左极限:当 x 从左侧接近 0 时,f(x) = x^2 + 1,因此 f(0^-) = 0^2 + 1 = 1。
- 右极限:当 x 从右侧接近 0 时,f(x) = x + 2,因此 f(0^+) = 0 + 2 = 2。
步骤 2:应用傅里叶级数的收敛定理
- 根据傅里叶级数的收敛定理,当函数在某点处不连续时,傅里叶级数在该点的和函数值等于该点处的左极限和右极限的平均值。
- 因此,S(0) = (f(0^-) + f(0^+)) / 2 = (1 + 2) / 2 = 3 / 2。
- 左极限:当 x 从左侧接近 0 时,f(x) = x^2 + 1,因此 f(0^-) = 0^2 + 1 = 1。
- 右极限:当 x 从右侧接近 0 时,f(x) = x + 2,因此 f(0^+) = 0 + 2 = 2。
步骤 2:应用傅里叶级数的收敛定理
- 根据傅里叶级数的收敛定理,当函数在某点处不连续时,傅里叶级数在该点的和函数值等于该点处的左极限和右极限的平均值。
- 因此,S(0) = (f(0^-) + f(0^+)) / 2 = (1 + 2) / 2 = 3 / 2。