题目
15.函数 (x,y)=x+(y)^3 在点(1,1)处沿方向 overrightarrow (i)=(3,-4) 的方向导数为 __
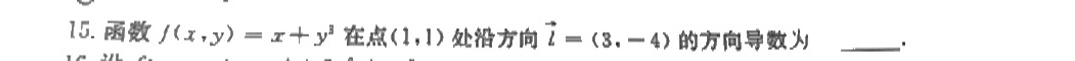
题目解答
答案

解析
步骤 1:计算方向向量的单位向量
方向向量 $\overrightarrow{l}=(3,-4)$ 的模长为 $\sqrt{3^2+(-4)^2}=\sqrt{9+16}=\sqrt{25}=5$。因此,方向向量的单位向量为 $\overrightarrow{u}=\left(\frac{3}{5},-\frac{4}{5}\right)$。
步骤 2:计算函数 $f(x,y)$ 在点 $(1,1)$ 处的偏导数
函数 $f(x,y)=x+y^3$ 在点 $(1,1)$ 处的偏导数为:
- $f_x(x,y)=\frac{\partial}{\partial x}(x+y^3)=1$
- $f_y(x,y)=\frac{\partial}{\partial y}(x+y^3)=3y^2$
因此,在点 $(1,1)$ 处,$f_x(1,1)=1$,$f_y(1,1)=3(1)^2=3$。
步骤 3:计算方向导数
方向导数为 $f_x(1,1)\cos\alpha+f_y(1,1)\cos\beta$,其中 $\cos\alpha=\frac{3}{5}$,$\cos\beta=-\frac{4}{5}$。因此,方向导数为:
$1\times\frac{3}{5}+3\times(-\frac{4}{5})=\frac{3}{5}-\frac{12}{5}=-\frac{9}{5}$。
方向向量 $\overrightarrow{l}=(3,-4)$ 的模长为 $\sqrt{3^2+(-4)^2}=\sqrt{9+16}=\sqrt{25}=5$。因此,方向向量的单位向量为 $\overrightarrow{u}=\left(\frac{3}{5},-\frac{4}{5}\right)$。
步骤 2:计算函数 $f(x,y)$ 在点 $(1,1)$ 处的偏导数
函数 $f(x,y)=x+y^3$ 在点 $(1,1)$ 处的偏导数为:
- $f_x(x,y)=\frac{\partial}{\partial x}(x+y^3)=1$
- $f_y(x,y)=\frac{\partial}{\partial y}(x+y^3)=3y^2$
因此,在点 $(1,1)$ 处,$f_x(1,1)=1$,$f_y(1,1)=3(1)^2=3$。
步骤 3:计算方向导数
方向导数为 $f_x(1,1)\cos\alpha+f_y(1,1)\cos\beta$,其中 $\cos\alpha=\frac{3}{5}$,$\cos\beta=-\frac{4}{5}$。因此,方向导数为:
$1\times\frac{3}{5}+3\times(-\frac{4}{5})=\frac{3}{5}-\frac{12}{5}=-\frac{9}{5}$。