题目
2、设函数 f(x)= ) a(e)^x+1,xleqslant 0 x+b, xgt 0 . x=0 可导,则a,b应该取何值?
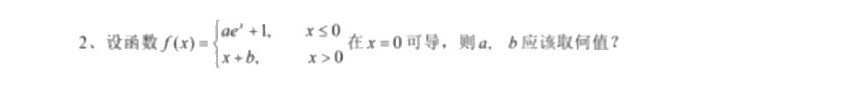
题目解答
答案

解析
考查要点:本题主要考查分段函数在分界点处的可导性条件,需要同时满足连续性和左右导数相等两个条件。
解题核心思路:
- 连续性条件:函数在$x=0$处连续,即左极限等于右极限且等于函数值$f(0)$。
- 可导性条件:函数在$x=0$处的左导数等于右导数。
破题关键点:
- 连续性方程:通过左右极限相等建立$a$与$b$的关系。
- 导数方程:分别求左右导数并令其相等,直接得到$a$的值。
步骤1:验证连续性
当$x \leqslant 0$时,$f(x) = a e^x + 1$,当$x > 0$时,$f(x) = x + b$。
连续性条件要求:
$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0)$
- 左极限:$\lim_{x \to 0^-} (a e^x + 1) = a e^0 + 1 = a + 1$
- 右极限:$\lim_{x \to 0^+} (x + b) = 0 + b = b$
- 函数值:$f(0) = a e^0 + 1 = a + 1$
因此,连续性条件给出方程:
$a + 1 = b \quad \text{(方程1)}$
步骤2:求左右导数并令其相等
左导数($x \to 0^-$):
$f(x) = a e^x + 1$的导数为$f'(x) = a e^x$,因此左导数为:
$f'_-(0) = a e^0 = a$
右导数($x \to 0^+$):
$f(x) = x + b$的导数为$f'(x) = 1$,因此右导数为:
$f'_+(0) = 1$
可导性条件要求:
$f'_-(0) = f'_+(0) \implies a = 1 \quad \text{(方程2)}$
步骤3:联立方程求解
将$a = 1$代入方程1:
$1 + 1 = b \implies b = 2$