(5) lim _(xarrow 1)dfrac (sqrt {5x-4)-sqrt (x)}(x-1);
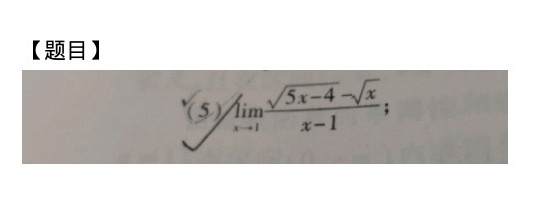
题目解答
答案

解析
考查要点:本题主要考查分式极限的求解方法,特别是处理0/0型不定式的技巧。关键在于通过分子有理化或洛必达法则消除不定式形式。
解题核心思路:
当直接代入$x=1$导致分母为0且分子为0时,需对分子进行有理化处理,将分式转化为可约简的形式,从而消去分母中的零因子。或者利用洛必达法则对分子分母分别求导,简化计算。
破题关键点:
- 识别0/0型不定式,选择合适的方法(有理化或洛必达法则)。
- 分子有理化时,通过乘以共轭表达式消去根号,约分后直接代入求值。
步骤1:分子有理化
将分子$\sqrt{5x-4} - \sqrt{x}$乘以共轭表达式$\sqrt{5x-4} + \sqrt{x}$,并同时对分母进行相同操作:
$\begin{aligned}\lim _{x\rightarrow 1}\dfrac {\sqrt {5x-4}-\sqrt {x}}{x-1} &= \lim _{x\rightarrow 1} \dfrac{(\sqrt{5x-4} - \sqrt{x})(\sqrt{5x-4} + \sqrt{x})}{(x-1)(\sqrt{5x-4} + \sqrt{x})} \\&= \lim _{x\rightarrow 1} \dfrac{(5x-4) - x}{(x-1)(\sqrt{5x-4} + \sqrt{x})} \\&= \lim _{x\rightarrow 1} \dfrac{4x-4}{(x-1)(\sqrt{5x-4} + \sqrt{x})}.\end{aligned}$
步骤2:约分简化
分子提取公因数$4$,分母保留$(x-1)$:
$\lim _{x\rightarrow 1} \dfrac{4(x-1)}{(x-1)(\sqrt{5x-4} + \sqrt{x})} = \lim _{x\rightarrow 1} \dfrac{4}{\sqrt{5x-4} + \sqrt{x}}.$
步骤3:代入求值
直接代入$x=1$:
$\sqrt{5 \cdot 1 -4} + \sqrt{1} = \sqrt{1} + 1 = 2, \quad \text{故极限值为} \dfrac{4}{2} = 2.$