题目
1.1计算下列各式.-|||-(1) (1+i)-(3-2i) ;-|||-(2) ((a-ib))^3 ;-|||-(3) dfrac (i)((i-1)(i-2)) =-|||-(4) dfrac (z-1)(z+1)(z=x+iyneq -1) -
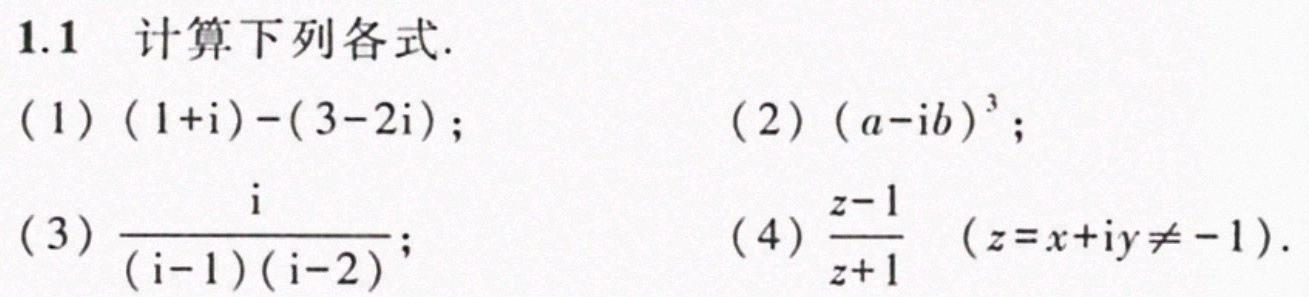
题目解答
答案
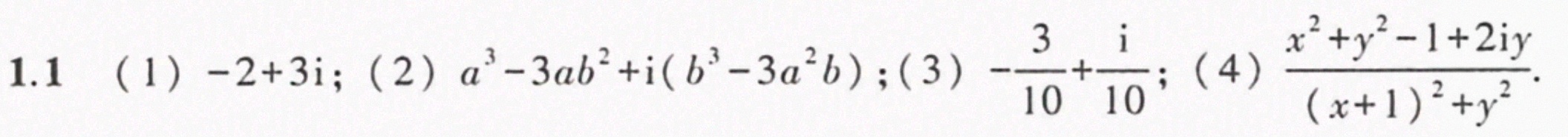
解析
步骤 1:计算 (1+i)-(3-2i)
将复数相减,实部与实部相减,虚部与虚部相减。
步骤 2:计算 ${(a-ib)}^{3}$
使用二项式定理展开立方,注意虚数单位i的性质。
步骤 3:计算 $\dfrac {i}{(i-1)(i-2)}$
先计算分母,然后进行复数除法。
步骤 4:计算 $\dfrac {z-1}{z+1}(z=x+iy\neq -1)$
将z代入,然后进行复数除法。
将复数相减,实部与实部相减,虚部与虚部相减。
步骤 2:计算 ${(a-ib)}^{3}$
使用二项式定理展开立方,注意虚数单位i的性质。
步骤 3:计算 $\dfrac {i}{(i-1)(i-2)}$
先计算分母,然后进行复数除法。
步骤 4:计算 $\dfrac {z-1}{z+1}(z=x+iy\neq -1)$
将z代入,然后进行复数除法。