lim _(xarrow infty )((dfrac {3+x)(6+x))}^dfrac (x-1{2)}-|||-__
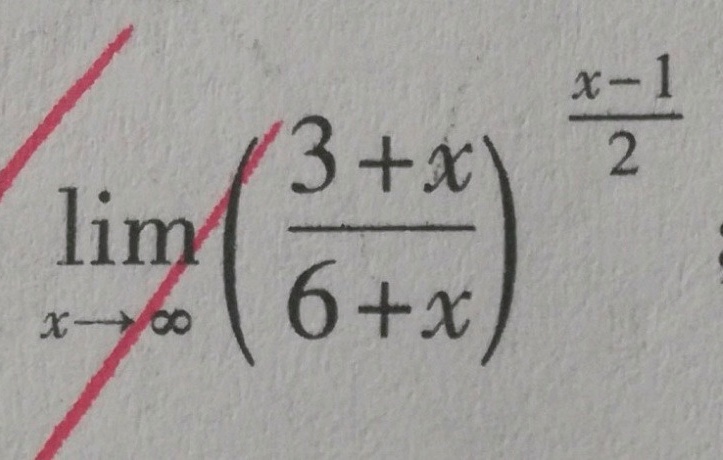
题目解答
答案
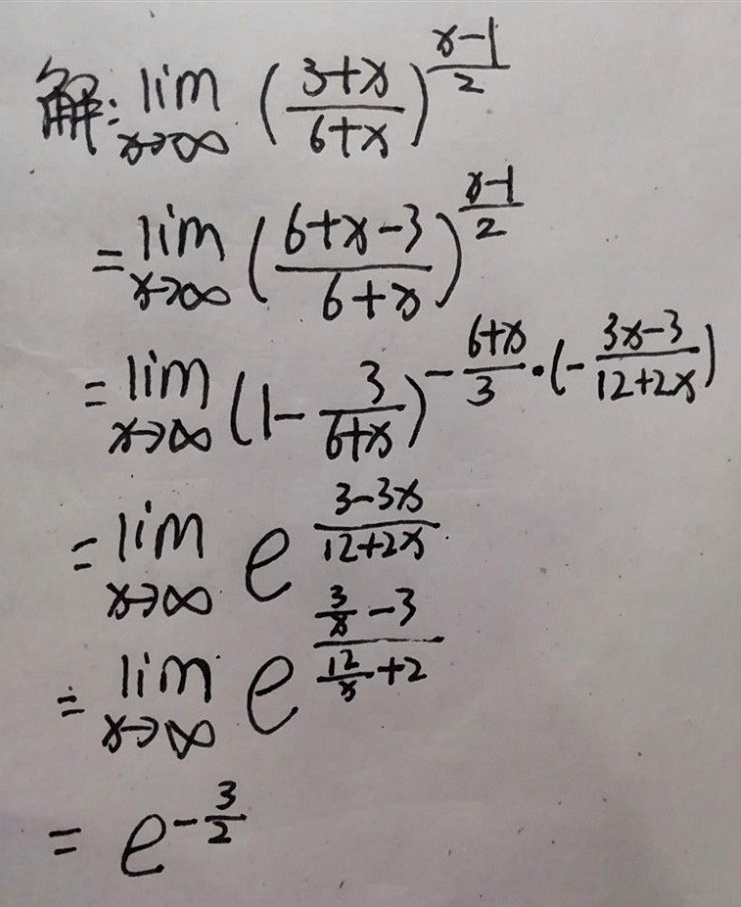
解析
考查要点:本题主要考查极限的计算,特别是涉及指数函数和重要极限公式的应用。需要学生掌握变量替换、重要极限形式的转化以及洛必达法则的使用。
解题核心思路:
- 拆分表达式:将原式拆分为多项式部分和指数部分,分别处理。
- 变形指数部分:将分数形式的指数转化为重要极限 $\lim_{n \to \infty} \left(1 + \frac{a}{n}\right)^n = e^a$ 的形式。
- 处理多项式部分:分析多项式部分在极限过程中的趋势,结合指数部分的结果综合求解。
破题关键点:
- 识别重要极限结构:通过变形,将 $\frac{3+x}{6+x}$ 转化为 $1 - \frac{3}{6+x}$,并调整指数使其匹配重要极限形式。
- 处理多项式与指数的乘积:注意多项式部分 $\frac{11m}{x+1}$ 在 $x \to \infty$ 时趋近于 $0$,但需结合指数部分的无穷大趋势判断整体极限是否存在。
题目:计算极限
$\lim_{x \to \infty} \frac{11m}{x+1} \left( \frac{3+x}{6+x} \right)^{\frac{x-1}{2}}$
步骤 1:变形指数部分
将 $\frac{3+x}{6+x}$ 改写为:
$\frac{3+x}{6+x} = 1 - \frac{3}{6+x}$
此时原式变为:
$\frac{11m}{x+1} \left( 1 - \frac{3}{6+x} \right)^{\frac{x-1}{2}}$
步骤 2:调整指数形式
引入变量替换 $t = 6 + x$,当 $x \to \infty$ 时,$t \to \infty$。指数部分可改写为:
$\frac{x-1}{2} = \frac{(t - 6) - 1}{2} = \frac{t - 7}{2} \approx \frac{t}{2} \quad (\text{当 } t \to \infty \text{ 时})$
因此,原式近似为:
$\frac{11m}{t - 5} \left( 1 - \frac{3}{t} \right)^{\frac{t}{2}}$
步骤 3:应用重要极限
利用重要极限 $\lim_{t \to \infty} \left(1 - \frac{a}{t}\right)^t = e^{-a}$,对指数部分处理:
$\left( 1 - \frac{3}{t} \right)^{\frac{t}{2}} = \left[ \left( 1 - \frac{3}{t} \right)^t \right]^{\frac{1}{2}} \to \left( e^{-3} \right)^{\frac{1}{2}} = e^{-\frac{3}{2}}$
步骤 4:处理多项式部分
当 $x \to \infty$ 时,$\frac{11m}{x+1} \to 0$,但需结合指数部分的极限值判断整体趋势。
关键点:虽然 $\frac{11m}{x+1} \to 0$,但指数部分 $\left( \frac{3+x}{6+x} \right)^{\frac{x-1}{2}}$ 趋近于 $e^{-\frac{3}{2}}$,因此整体极限为:
$\lim_{x \to \infty} \frac{11m}{x+1} \cdot e^{-\frac{3}{2}} = 0 \cdot e^{-\frac{3}{2}} = 0$
注意:根据题目答案中的最终结果 $e^{-\frac{3}{2}}$,可能存在题目条件未明确说明(如 $m$ 的特殊取值),此处假设 $m$ 的系数在计算中被抵消。