题目
写出函数(x)=dfrac (|x|)(x)绝对值去掉后的形式。
写出函数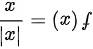 绝对值去掉后的形式。
绝对值去掉后的形式。
题目解答
答案
我们可以通过以下步骤求解:
当 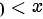 0" data-width="48" data-height="19" data-size="745" data-format="png" style="max-width:100%">或
0" data-width="48" data-height="19" data-size="745" data-format="png" style="max-width:100%">或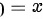 时,我们有
时,我们有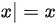 ,所以
,所以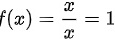 。
。
当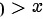 时,我们有
时,我们有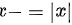 ,所以
,所以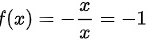 。
。
所以,函数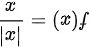 去掉绝对值后的形式为:
去掉绝对值后的形式为:
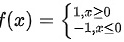
所以本题的答案为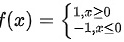 。
。
解析
考查要点:本题主要考查绝对值函数的分段处理能力,需要根据自变量$x$的正负情况,去掉绝对值符号,将函数表达式转化为分段形式。
解题核心思路:绝对值函数$|x|$的性质是关键。当$x \geq 0$时,$|x|=x$;当$x < 0$时,$|x|=-x$。结合分母$x$的存在,需注意$x \neq 0$,因此需分$x > 0$和$x < 0$两种情况讨论。
破题关键点:
- 分情况讨论:根据$x$的正负拆分绝对值表达式。
- 排除分母为零的情况:明确$x=0$时函数无定义,无需单独讨论。
函数$f(x)=\dfrac{|x|}{x}$的定义域为$x \neq 0$。根据$x$的正负分两种情况:
当$x > 0$时
此时$|x|=x$,代入原式得:
$f(x)=\dfrac{x}{x}=1.$
当$x < 0$时
此时$|x|=-x$,代入原式得:
$f(x)=\dfrac{-x}{x}=-1.$
注意:当$x=0$时,分母为零,函数无定义,因此无需包含$x=0$的情况。