题目
5.(2011)讨论函数 f(x)= ^2) xneq 0 0 x=0 . 在 x=0 处的可导性
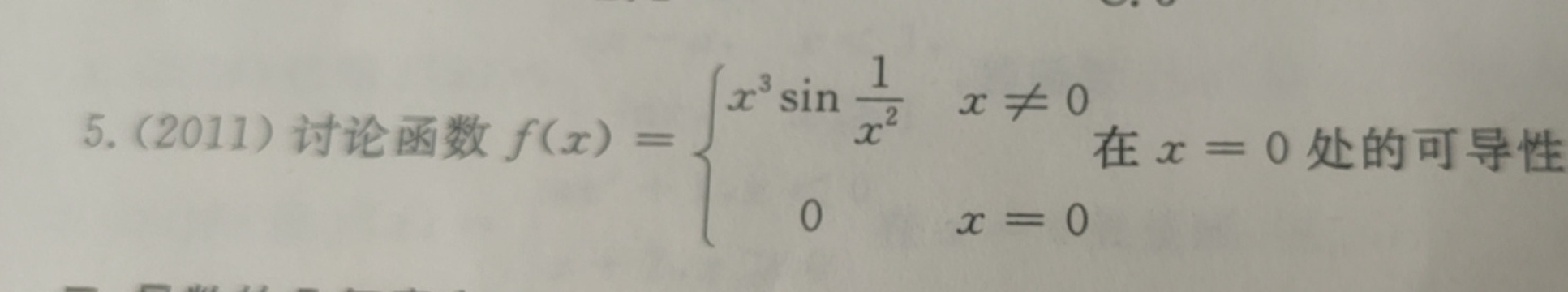
题目解答
答案
解析
本题考察分段函数在分段点处的可导性,关键是利用导数的定义判断极限是否存在。
步骤1:回顾导数定义
函数$f(x)$在$x=0$处的导数定义为:
$f'(0)=\lim_{x \to 0} \frac{f(x)-f(0)}{x-0}$
已知$f(0)=0$,且$x \neq 0$时$f(x)=x^3\sin\frac{1}{x^2}$,代入得:
$f'(0)=\lim_{x \to 0} \frac{x^3\sin\frac{1}{x^2}-0}{x}=\lim_{x \to 0} x^2\sin\frac{1}{x^2}$
步骤2:分析极限存在性
需判断$\lim_{x \to 0} x^2\sin\frac{1}{x^2}$是否存在。
根据三角函数性质,$\sin\theta$的值域为$[-1,1]$,故:
$-x^2 \leq x^2\sin\frac{1}{x^2} \leq x^2$
当$x \to 0$时,$-x^2 \to 0$且$x^2 \to 0$,由夹逼准则:
$\lim_{x \to 0} x^2\sin\frac{1}{x^2}=0$
结论
极限存在,故$f(x)$在$x=0$处可导,且$f'(0)=0$。