题目
设随机变量X和Y的联合分布律为X -1-|||-Y 0 1-|||--1 dfrac (1)(8) dfrac (1)(8) dfrac (1)(8)-|||-0 dfrac (1)(8) 0 dfrac (1)(8)-|||-1 dfrac (1)(8) dfrac (1)(8) dfrac (1)(8)验证:X和Y不相关,但X和Y不是相互独立的.
设随机变量X和Y的联合分布律为
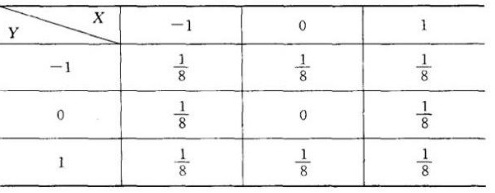
验证:X和Y不相关,但X和Y不是相互独立的.
题目解答
答案
解: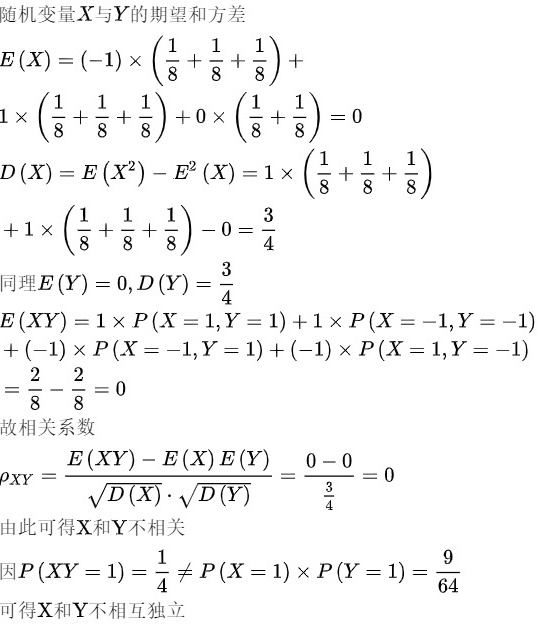
解析
步骤 1:计算边缘分布律
首先,我们需要计算随机变量X和Y的边缘分布律。边缘分布律是联合分布律在某一变量上的边缘分布,即固定一个变量,对另一个变量求和。
对于X的边缘分布律,我们有:
- P(X=-1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
- P(X=0) = $\dfrac {1}{8} + 0 + \dfrac {1}{8} = \dfrac {2}{8} = \dfrac {1}{4}$
- P(X=1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
对于Y的边缘分布律,我们有:
- P(Y=-1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
- P(Y=0) = $\dfrac {1}{8} + 0 + \dfrac {1}{8} = \dfrac {2}{8} = \dfrac {1}{4}$
- P(Y=1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
步骤 2:计算期望值
接下来,我们计算随机变量X和Y的期望值。
- E(X) = (-1) * $\dfrac {3}{8}$ + 0 * $\dfrac {1}{4}$ + 1 * $\dfrac {3}{8}$ = 0
- E(Y) = (-1) * $\dfrac {3}{8}$ + 0 * $\dfrac {1}{4}$ + 1 * $\dfrac {3}{8}$ = 0
步骤 3:计算协方差
然后,我们计算随机变量X和Y的协方差。
- Cov(X,Y) = E(XY) - E(X)E(Y)
- E(XY) = (-1)(-1) * $\dfrac {1}{8}$ + (-1)(0) * $\dfrac {1}{8}$ + (-1)(1) * $\dfrac {1}{8}$ + (0)(-1) * $\dfrac {1}{8}$ + (0)(0) * 0 + (0)(1) * $\dfrac {1}{8}$ + (1)(-1) * $\dfrac {1}{8}$ + (1)(0) * $\dfrac {1}{8}$ + (1)(1) * $\dfrac {1}{8}$ = 0
- Cov(X,Y) = 0 - 0 * 0 = 0
步骤 4:验证不相关性
由于Cov(X,Y) = 0,所以X和Y不相关。
步骤 5:验证独立性
最后,我们验证X和Y是否独立。如果X和Y独立,那么对于所有的x和y,P(X=x,Y=y) = P(X=x)P(Y=y)。我们检查一个例子:
- P(X=-1,Y=-1) = $\dfrac {1}{8}$
- P(X=-1)P(Y=-1) = $\dfrac {3}{8} * \dfrac {3}{8} = \dfrac {9}{64}$
由于$\dfrac {1}{8} \neq \dfrac {9}{64}$,所以X和Y不是相互独立的。
首先,我们需要计算随机变量X和Y的边缘分布律。边缘分布律是联合分布律在某一变量上的边缘分布,即固定一个变量,对另一个变量求和。
对于X的边缘分布律,我们有:
- P(X=-1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
- P(X=0) = $\dfrac {1}{8} + 0 + \dfrac {1}{8} = \dfrac {2}{8} = \dfrac {1}{4}$
- P(X=1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
对于Y的边缘分布律,我们有:
- P(Y=-1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
- P(Y=0) = $\dfrac {1}{8} + 0 + \dfrac {1}{8} = \dfrac {2}{8} = \dfrac {1}{4}$
- P(Y=1) = $\dfrac {1}{8} + \dfrac {1}{8} + \dfrac {1}{8} = \dfrac {3}{8}$
步骤 2:计算期望值
接下来,我们计算随机变量X和Y的期望值。
- E(X) = (-1) * $\dfrac {3}{8}$ + 0 * $\dfrac {1}{4}$ + 1 * $\dfrac {3}{8}$ = 0
- E(Y) = (-1) * $\dfrac {3}{8}$ + 0 * $\dfrac {1}{4}$ + 1 * $\dfrac {3}{8}$ = 0
步骤 3:计算协方差
然后,我们计算随机变量X和Y的协方差。
- Cov(X,Y) = E(XY) - E(X)E(Y)
- E(XY) = (-1)(-1) * $\dfrac {1}{8}$ + (-1)(0) * $\dfrac {1}{8}$ + (-1)(1) * $\dfrac {1}{8}$ + (0)(-1) * $\dfrac {1}{8}$ + (0)(0) * 0 + (0)(1) * $\dfrac {1}{8}$ + (1)(-1) * $\dfrac {1}{8}$ + (1)(0) * $\dfrac {1}{8}$ + (1)(1) * $\dfrac {1}{8}$ = 0
- Cov(X,Y) = 0 - 0 * 0 = 0
步骤 4:验证不相关性
由于Cov(X,Y) = 0,所以X和Y不相关。
步骤 5:验证独立性
最后,我们验证X和Y是否独立。如果X和Y独立,那么对于所有的x和y,P(X=x,Y=y) = P(X=x)P(Y=y)。我们检查一个例子:
- P(X=-1,Y=-1) = $\dfrac {1}{8}$
- P(X=-1)P(Y=-1) = $\dfrac {3}{8} * \dfrac {3}{8} = \dfrac {9}{64}$
由于$\dfrac {1}{8} \neq \dfrac {9}{64}$,所以X和Y不是相互独立的。