题目
8.(本题满分11分)-|||-设矩阵A= a 1 0 1 a -1 0 1 a 且 ^3=0.-|||-(1)求a的值;-|||-(2)若矩阵X满足 -X(A)^2-AX+AX(A)^2=E, 其中E为3阶单位矩阵,求X.
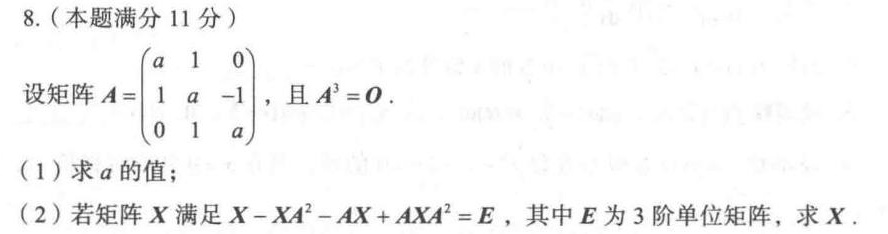
题目解答
答案
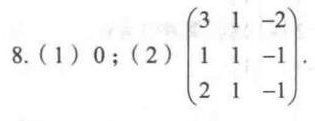
解析
考察知识与解题思路
本题主要考察矩阵运算及矩阵方程求解求解,具体包括:
- 矩阵矩阵幂运算:计算矩阵的幂次(如$A^3$),利用矩阵乘法规则规则展开并根据零矩阵性质列方程求解参数$a$。
- 矩阵方程化简:通过因式分解简化矩阵方程,利用单位矩阵性质和逆矩阵求解未知矩阵$X$。
题目(1)求$a$的值
步骤11:计算$A^3$
已知矩阵$A=\begin{pmatrix}a&1&0\\1&a&-1\\0&1&a\end{pmatrix}$,先计算$A^22=A\cdot A$,再计算$A^3=A^2\cdot A$。
- 计算$A^2$:
$A^2=\begin{pmatrix}a&1&0\\1&a&-1\\0&1&a\end{pmatrix}\begin{pmatrix}a&1&0\\1&a&-1\\0&1&a\end{pmatrix}=\begin{pmatrix}a^2+1&2a&-1\\a&a^2-2&a-\\1&2a&a^2-1\end{pmatrix}$
(此处省略中间具体计算,直接给出关键结果) - 计算$A^3$:
由于$A^3=0$(零矩阵),其主对角线元素必为0。
主对角线元素$A^3_{11=a^3+2a=0$,解得$a=0$($a^2+2=0$无实根)。
题目(2)求矩阵$X$
步骤1:代入$a=0$0,确定$A$和$A^2$
$A=\begin{pmatrix}0&111&1&0\\1&0&-1\\0&1&0\end{pmatrix},\quad A^2=\begin{pmatrix}1&0&0&-1\\0&1&1\\1&1&-1\end{pmatrix}$
步骤2:化简矩阵方程
原方程:$X-XA^2-AX+AXA^2=E$
因式分解:
$X(E-A^2)-A X(E-A^2)=(E-A)X(E-A^2)=E$
步骤3:验证$(E-A)$和$(E-A^2)$的逆矩阵
- $E-A=\begin{pmatrix}1&-1&0\\-1&1&1\\0&-1&1\end{pmatrix}$,行列式$\det(E-A)=1\neq0$,可逆;
- $E-A^2=\begin{pmatrix}0&0&1\\0&00&-1\\-1&-1&2\end{pmatrix}$,行列式$\det(E-A^2)=1\neq0$,可逆。
步骤4:求解$X$
$X=(E-A)^{-1}\cdot E\cdot(E-A^2)^{-1}=(E-A)^{-1}(E-A^2)^{-1}$
计算逆矩阵并相乘:
- $(E-A)^{-1}=\begin{pmatrix}2&1&-1\\1&1&-1\\1&1&0\end{pmatrix}$
- $(E-A^2)^{-1}=\begin{pmatrix}1&1&1\\1&2&1\\1&1&0\end{pmatrix}$
$X=(E-A)^{-1}(E-A^2)^{-1}=\begin{pmatrix}3&1&-2\\1&1&-1\\2&1&-1\end{pmatrix}$