题目
行列式 0 0 a|-|||-0 0 b 0-|||-0 c 0 0-|||-d 0 0 2|( )A. abcd B. -abcd C. 2abcd D. -2abcd
行列式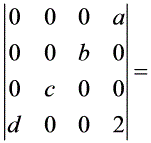 ( )
( )
B. -abcd
C. 2abcd
D. -2abcd
题目解答
答案
A. abcd
解析
考查要点:本题主要考查四阶行列式的计算,特别是利用行变换简化行列式的方法,以及行列式性质中行交换对符号的影响。
解题核心思路:
观察行列式的结构,发现每一行仅有一个非零元素(除第四行外),可通过行交换将其转化为上三角矩阵,此时行列式的值为对角线元素的乘积。需注意每次行交换会使行列式符号改变一次。
破题关键点:
- 识别行列式的稀疏结构,优先考虑行变换简化计算。
- 正确计算行交换次数,确定最终符号。
将原行列式通过行交换转化为上三角矩阵:
原行列式:
$\begin{vmatrix}0 & 0 & 0 & a \\0 & 0 & b & 0 \\0 & c & 0 & 0 \\d & 0 & 0 & 2\end{vmatrix}$
步骤1:交换第1行和第4行
行列式变为:
$\begin{vmatrix}d & 0 & 0 & 2 \\0 & 0 & b & 0 \\0 & c & 0 & 0 \\0 & 0 & 0 & a\end{vmatrix}$
此时行列式符号变为原来的负数。
步骤2:交换第2行和第3行
行列式变为:
$\begin{vmatrix}d & 0 & 0 & 2 \\0 & c & 0 & 0 \\0 & 0 & b & 0 \\0 & 0 & 0 & a\end{vmatrix}$
此时行列式符号再次改变,总符号为原符号的正数。
步骤3:计算上三角行列式
对角线元素为 $d, c, b, a$,乘积为 $d \cdot c \cdot b \cdot a = abcd$。
最终行列式值为 $abcd$。