题目
某企业在雇佣x名技术工人、y名非技术工人时，产品的产量Q=-8x^2+12xy-3y^2，若企业只能雇佣230人，则该雇佣多少技术与非技术工人才能使产量Q最大？
某企业在雇佣x名技术工人、y名非技术工人时，产品的产量Q=$$-8x^2+12xy-3y^2$$，若企业只能雇佣230人，则该雇佣多少技术与非技术工人才能使产量Q最大？
题目解答
答案
x+y=230
y=230-x
Q=-8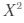
+12X(230-X)-3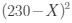
=-23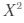+4140X-158700
=-23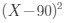
+27600
当x=90时
Q最大=27600
230-90=140(人)
答：雇用90名技术工人，140名非技术工人是才能使产量最大。
解析
步骤 1：确定约束条件
企业只能雇佣230人，即x+y=230。这意味着y=230-x。
步骤 2：将约束条件代入产量函数
将y=230-x代入产量函数Q=$$-8x^2+12xy-3y^2$$，得到Q关于x的函数。
步骤 3：求导数并找到极值点
对Q关于x的函数求导，找到导数为0的点，即产量Q的最大值点。
步骤 4：验证极值点
验证该点是否为最大值点，可以通过二阶导数测试或观察函数的性质。
步骤 5：计算y的值
根据x的值，计算y的值，即非技术工人的数量。
企业只能雇佣230人，即x+y=230。这意味着y=230-x。
步骤 2：将约束条件代入产量函数
将y=230-x代入产量函数Q=$$-8x^2+12xy-3y^2$$，得到Q关于x的函数。
步骤 3：求导数并找到极值点
对Q关于x的函数求导，找到导数为0的点，即产量Q的最大值点。
步骤 4：验证极值点
验证该点是否为最大值点，可以通过二阶导数测试或观察函数的性质。
步骤 5：计算y的值
根据x的值，计算y的值，即非技术工人的数量。