题目
(5) _(n)=det((a)_(v)), 其中 _(i)=|i-j|;
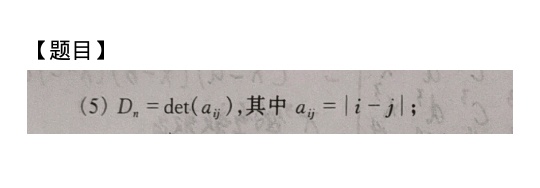
题目解答
答案

解析
步骤 1:定义行列式
行列式 ${D}_{n}$ 是一个 $n \times n$ 的矩阵,其中每个元素 ${a}_{ij} = |i-j|$,即第 $i$ 行第 $j$ 列的元素等于 $i$ 和 $j$ 的绝对差值。
步骤 2:构造行列式
构造行列式 ${D}_{n}$ 的形式如下:
$$
{D}_{n} = \begin{vmatrix}
0 & 1 & 2 & \cdots & n-2 & n-1 \\
1 & 0 & 1 & \cdots & n-3 & n-2 \\
2 & 1 & 0 & \cdots & n-4 & n-3 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
n-2 & n-3 & n-4 & \cdots & 0 & 1 \\
n-1 & n-2 & n-3 & \cdots & 1 & 0
\end{vmatrix}
$$
步骤 3:行列式变换
为了简化行列式,我们进行行变换。将第 $i$ 行减去第 $i+1$ 行,从第 $1$ 行到第 $n-1$ 行依次进行,得到:
$$
{D}_{n} = \begin{vmatrix}
-1 & 1 & 1 & \cdots & 1 & 1 \\
1 & -1 & 1 & \cdots & 1 & 1 \\
1 & 1 & -1 & \cdots & 1 & 1 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
1 & 1 & 1 & \cdots & -1 & 1 \\
1 & 1 & 1 & \cdots & 1 & 0
\end{vmatrix}
$$
步骤 4:行列式计算
观察行列式,可以发现除了最后一行和最后一列外,其余元素都是 $-1$ 或 $1$。最后一行和最后一列的元素都是 $1$,最后一列的最后一个元素是 $0$。因此,行列式可以进一步简化为:
$$
{D}_{n} = (-1)^{n-1} \begin{vmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & -1 & 1 & \cdots & 1 \\
1 & 1 & -1 & \cdots & 1 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & 1 & 1 & \cdots & -1
\end{vmatrix}
$$
这个行列式是一个特殊的行列式,可以通过递推公式计算。对于 $n \geq 2$,行列式 ${D}_{n}$ 的值为:
$$
{D}_{n} = (-1)^{n-1} (n-1) 2^{n-2}
$$
行列式 ${D}_{n}$ 是一个 $n \times n$ 的矩阵,其中每个元素 ${a}_{ij} = |i-j|$,即第 $i$ 行第 $j$ 列的元素等于 $i$ 和 $j$ 的绝对差值。
步骤 2:构造行列式
构造行列式 ${D}_{n}$ 的形式如下:
$$
{D}_{n} = \begin{vmatrix}
0 & 1 & 2 & \cdots & n-2 & n-1 \\
1 & 0 & 1 & \cdots & n-3 & n-2 \\
2 & 1 & 0 & \cdots & n-4 & n-3 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
n-2 & n-3 & n-4 & \cdots & 0 & 1 \\
n-1 & n-2 & n-3 & \cdots & 1 & 0
\end{vmatrix}
$$
步骤 3:行列式变换
为了简化行列式,我们进行行变换。将第 $i$ 行减去第 $i+1$ 行,从第 $1$ 行到第 $n-1$ 行依次进行,得到:
$$
{D}_{n} = \begin{vmatrix}
-1 & 1 & 1 & \cdots & 1 & 1 \\
1 & -1 & 1 & \cdots & 1 & 1 \\
1 & 1 & -1 & \cdots & 1 & 1 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
1 & 1 & 1 & \cdots & -1 & 1 \\
1 & 1 & 1 & \cdots & 1 & 0
\end{vmatrix}
$$
步骤 4:行列式计算
观察行列式,可以发现除了最后一行和最后一列外,其余元素都是 $-1$ 或 $1$。最后一行和最后一列的元素都是 $1$,最后一列的最后一个元素是 $0$。因此,行列式可以进一步简化为:
$$
{D}_{n} = (-1)^{n-1} \begin{vmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & -1 & 1 & \cdots & 1 \\
1 & 1 & -1 & \cdots & 1 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & 1 & 1 & \cdots & -1
\end{vmatrix}
$$
这个行列式是一个特殊的行列式,可以通过递推公式计算。对于 $n \geq 2$,行列式 ${D}_{n}$ 的值为:
$$
{D}_{n} = (-1)^{n-1} (n-1) 2^{n-2}
$$