题目
7.试问下列命题是否成立?(1)A-(B-C)=(A-B)-C;(2)A-(B-C)=(A-B)-C;(3)A-(B-C)=(A-B)-C;(4)A-(B-C)=(A-B)-C
7.试问下列命题是否成立?
(1)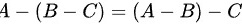 ;
;
(2)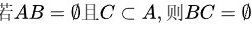 ;
;
(3)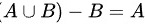 ;
;
(4)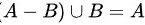
题目解答
答案
解:(1)不成立,∵(1)式右端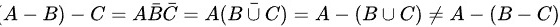
(3)式不成立,∵(3)式右端
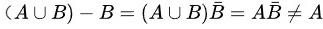
(4)式不成立,∵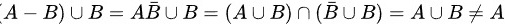
只有(2)式成立,因为互不相容的两个集合的子集也互不相容。
解析
步骤 1:分析命题(1)
命题(1)是关于集合的减法运算。我们首先需要理解集合减法的定义,即$A-B$表示集合$A$中去掉集合$B$中的元素后剩下的元素组成的集合。因此,$A-(B-C)$表示先从集合$B$中去掉集合$C$的元素,然后从集合$A$中去掉剩余的元素。而$(A-B)-C$表示先从集合$A$中去掉集合$B$的元素,然后从剩余的集合中去掉集合$C$的元素。这两个表达式并不一定相等,因为集合减法不满足结合律。
步骤 2:分析命题(2)
命题(2)是关于集合的交集运算。给定条件$AB=0$,表示集合$A$和集合$B$的交集为空集,即$A$和$B$互不相容。另外,条件$CCA$表示集合$C$是集合$A$的子集。由于$A$和$B$互不相容,$C$作为$A$的子集,也必然与$B$互不相容,即$BC=0$。
步骤 3:分析命题(3)
命题(3)是关于集合的并集和减法运算。$(A\cup B)-B$表示先将集合$A$和集合$B$合并,然后从合并后的集合中去掉集合$B$的元素。这相当于只保留集合$A$中不属于集合$B$的元素,即$A-B$。因此,$(A\cup B)-B$不等于$A$,除非$B$是空集。
步骤 4:分析命题(4)
命题(4)是关于集合的减法和并集运算。$(A-B)\cup B$表示先从集合$A$中去掉集合$B$的元素,然后将剩余的集合与集合$B$合并。这相当于将集合$A$中不属于集合$B$的元素与集合$B$合并,即$A$。因此,$(A-B)\cup B$等于$A$。
命题(1)是关于集合的减法运算。我们首先需要理解集合减法的定义,即$A-B$表示集合$A$中去掉集合$B$中的元素后剩下的元素组成的集合。因此,$A-(B-C)$表示先从集合$B$中去掉集合$C$的元素,然后从集合$A$中去掉剩余的元素。而$(A-B)-C$表示先从集合$A$中去掉集合$B$的元素,然后从剩余的集合中去掉集合$C$的元素。这两个表达式并不一定相等,因为集合减法不满足结合律。
步骤 2:分析命题(2)
命题(2)是关于集合的交集运算。给定条件$AB=0$,表示集合$A$和集合$B$的交集为空集,即$A$和$B$互不相容。另外,条件$CCA$表示集合$C$是集合$A$的子集。由于$A$和$B$互不相容,$C$作为$A$的子集,也必然与$B$互不相容,即$BC=0$。
步骤 3:分析命题(3)
命题(3)是关于集合的并集和减法运算。$(A\cup B)-B$表示先将集合$A$和集合$B$合并,然后从合并后的集合中去掉集合$B$的元素。这相当于只保留集合$A$中不属于集合$B$的元素,即$A-B$。因此,$(A\cup B)-B$不等于$A$,除非$B$是空集。
步骤 4:分析命题(4)
命题(4)是关于集合的减法和并集运算。$(A-B)\cup B$表示先从集合$A$中去掉集合$B$的元素,然后将剩余的集合与集合$B$合并。这相当于将集合$A$中不属于集合$B$的元素与集合$B$合并,即$A$。因此,$(A-B)\cup B$等于$A$。