6.设A= (} 2& 0& 0 0& 3& 5 0& 1& 4 ) . ,且 AB=A+B ,求 +B. 。
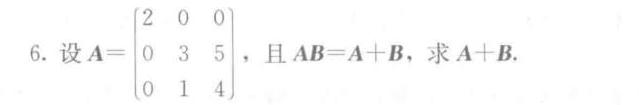
题目解答
答案
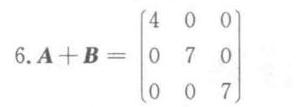
解析
考查要点:本题主要考查矩阵方程的求解,涉及矩阵乘法、分块矩阵的性质以及方程组的解法。
解题核心思路:
- 观察矩阵结构:矩阵A具有分块上三角结构,左上角为1×1块,右下角为2×2块。利用分块矩阵的乘法规律,可将问题分解为更简单的子问题。
- 方程变形:将原方程$AB = A + B$变形为$B(A - I) = A$,若$A - I$可逆,则$B = A(A - I)^{-1}$。但直接计算逆矩阵较复杂,因此通过分块处理简化运算。
- 分块求解:分别求解左上角块和右下角块的方程,最终得到$A + B$的结构。
破题关键点:
- 分块矩阵的分解:将矩阵B假设为与A相同的分块结构,简化乘法运算。
- 块内方程组求解:通过对应位置元素相等,建立方程组求解未知数。
步骤1:分解矩阵结构
矩阵$A$可分解为分块形式:
$A = \begin{bmatrix}2 & \mathbf{0}^T \\\mathbf{0} & \begin{bmatrix}3 & 5 \\ 1 & 4\end{bmatrix}
\end{bmatrix}$
假设矩阵$B$具有相同分块结构:
$B = \begin{bmatrix}b_{11} & \mathbf{0}^T \\\mathbf{0} & \begin{bmatrix}b_{22} & b_{23} \\ b_{32} & b_{33}\end{bmatrix}
\end{bmatrix}$
步骤2:求解左上角块
根据方程$AB = A + B$,左上角块满足:
$2b_{11} = 2 + b_{11} \implies b_{11} = 2$
因此,$A + B$的左上角块为$2 + 2 = 4$。
步骤3:求解右下角块
设$A$的右下角块为$\begin{bmatrix}3 & 5 \\ 1 & 4\end{bmatrix}$,$B$的右下角块为$\begin{bmatrix}b_{22} & b_{23} \\ b_{32} & b_{33}\end{bmatrix}$。根据方程$AB = A + B$,对应元素满足:
-
(1,1)位置:
$3b_{22} + 5b_{32} = 3 + b_{22} \implies 2b_{22} + 5b_{32} = 3$ -
(2,1)位置:
$b_{22} + 4b_{32} = 1 + b_{32} \implies b_{22} + 3b_{32} = 1$
解得:$b_{32} = -1$,$b_{22} = 4$。 -
(1,2)位置:
$3b_{23} + 5b_{33} = 5 + b_{23} \implies 2b_{23} + 5b_{33} = 5$ -
(2,2)位置:
$b_{23} + 4b_{33} = 4 + b_{33} \implies b_{23} + 3b_{33} = 4$
解得:$b_{33} = 3$,$b_{23} = -5$。
因此,$B$的右下角块为$\begin{bmatrix}4 & -5 \\ -1 & 3\end{bmatrix}$,对应$A + B$的右下角块为:
$\begin{bmatrix}3 + 4 & 5 + (-5) \\ 1 + (-1) & 4 + 3\end{bmatrix} = \begin{bmatrix}7 & 0 \\ 0 & 7\end{bmatrix}$