题目
求极限lim _(narrow infty )sqrt [n](1+{a)^n+(a)^2n}(agt 0)
求极限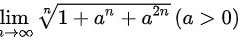
题目解答
答案
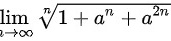
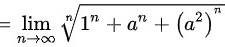
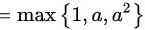
当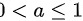 时
时
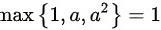
当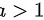 时
时
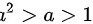
∴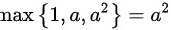
∴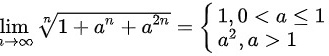
故答案为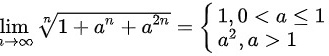
解析
考查要点:本题主要考查n次根号下多项式的极限,需要根据参数$a$的不同取值范围,确定主导项并应用极限性质。
解题核心思路:
当$n \rightarrow \infty$时,表达式$\sqrt[n]{1 + a^n + a^{2n}}$的极限由三个项中的最大值决定。通过比较$1$、$a^n$、$a^{2n}$的大小关系,分情况讨论$a$的取值范围,最终确定极限值。
破题关键点:
- 分情况讨论:根据$a$与$1$的大小关系,将问题划分为$0 < a \leq 1$和$a > 1$两种情形。
- 提取主导项:在每种情形下,找到增长最快的项,将其作为主导项,剩余项的影响可忽略。
情形1:当$0 < a \leq 1$时
-
分析项的大小:
- $a \leq 1$,因此$a^n \rightarrow 0$,$a^{2n} \rightarrow 0$(当$n \rightarrow \infty$时)。
- 此时$1$是最大的项,即$\max\{1, a, a^2\} = 1$。
-
极限计算:
$\sqrt[n]{1 + a^n + a^{2n}} = \sqrt[n]{1 \cdot \left(1 + a^n + a^{2n}\right)} = 1 \cdot \sqrt[n]{1 + a^n + a^{2n}}$
由于$a^n$和$a^{2n}$趋近于$0$,括号内整体趋近于$1$,故极限为$1$。
情形2:当$a > 1$时
-
分析项的大小:
- $a > 1$,因此$a^{2n}$增长最快,是最大的项,即$\max\{1, a, a^2\} = a^2$。
-
极限计算:
$\sqrt[n]{1 + a^n + a^{2n}} = \sqrt[n]{a^{2n} \left(1 + a^{-n} + a^{-2n}\right)} = a^2 \cdot \sqrt[n]{1 + a^{-n} + a^{-2n}}$
由于$a^{-n} \rightarrow 0$,$a^{-2n} \rightarrow 0$,括号内整体趋近于$1$,故极限为$a^2$。