题目
1.设随机变量X的分布律为-|||- X=k =cdfrac ({lambda )^k}(k!) =1,2, ..... lambda gt 0,-|||-求常数c的值.

题目解答
答案
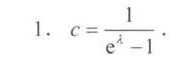
解析
考查要点:本题主要考查概率分布的归一化条件,即所有可能取值的概率之和等于1。需要利用指数函数的泰勒展开式来简化求和过程。
解题核心思路:
- 根据概率分布的归一化条件,写出总概率为1的方程。
- 将求和式与指数函数的展开式关联,通过减去多余项(k=0时的项)得到最终表达式。
- 解方程求出常数c的值。
破题关键点:
- 识别指数函数展开式:$\sum_{k=0}^{\infty} \frac{\lambda^k}{k!} = e^{\lambda}$。
- 调整求和下界:题目中求和从$k=1$开始,需从指数展开式中减去$k=0$的项(即1)。
根据概率分布的归一化条件,所有可能取值的概率之和为1:
$\sum_{k=1}^{\infty} P\{X=k\} = \sum_{k=1}^{\infty} c \cdot \frac{\lambda^k}{k!} = 1.$
步骤1:关联指数函数展开式
指数函数$e^{\lambda}$的泰勒展开式为:
$e^{\lambda} = \sum_{k=0}^{\infty} \frac{\lambda^k}{k!}.$
步骤2:调整求和范围
题目中的求和从$k=1$开始,因此:
$\sum_{k=1}^{\infty} \frac{\lambda^k}{k!} = e^{\lambda} - \frac{\lambda^0}{0!} = e^{\lambda} - 1.$
步骤3:代入归一化条件
将上述结果代入原方程:
$c \cdot (e^{\lambda} - 1) = 1.$
步骤4:解方程求c
解得:
$c = \frac{1}{e^{\lambda} - 1}.$