题目
A.B.C 均为 n 阶对称矩阵,下列结论正确的是()AB为对称矩阵当AB=BA时,AB为对称矩阵A+B为对称矩阵A-B为对称矩阵对任何n阶矩阵P,^TAP为对称矩阵
A.B.C 均为 n 阶对称矩阵,下列结论正确的是()
- AB为对称矩阵
- 当AB=BA时,AB为对称矩阵
- A+B为对称矩阵
- A-B为对称矩阵
- 对任何n阶矩阵P,
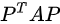 为对称矩阵
为对称矩阵
题目解答
答案
∵A.B均为n阶对称矩阵
∴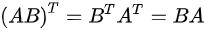
当且仅当AB=BA时,
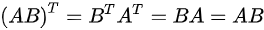
∴B正确,A不正确
∵A.B均为n阶对称矩阵
∴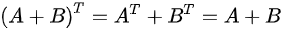
∴C正确
∵A.B均为n阶对称矩阵
∴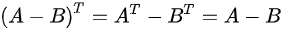
∴D正确
∵A均为n阶对称矩阵
∴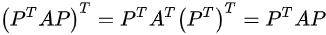
∴对于任何n阶矩阵P,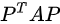 均为对阵矩阵
均为对阵矩阵
∴E正确
∴答案为BCDE
解析
考查要点:本题主要考查对称矩阵的性质及其运算后的对称性判断,涉及矩阵转置、乘法、加减法以及相似变换后的对称性。
解题核心思路:
- 对称矩阵的定义:若矩阵$A$满足$A^T = A$,则$A$为对称矩阵。
- 运算后的对称性判断:
- 乘法:$AB$的对称性取决于$A$与$B$是否可交换(即$AB=BA$)。
- 加减法:对称矩阵的加减结果仍为对称矩阵。
- 相似变换:对称矩阵经过任意矩阵$P$的相似变换$P^TAP$后仍保持对称性。
破题关键点:
- 转置运算的分配律:$(AB)^T = B^T A^T$,$(A+B)^T = A^T + B^T$,$(A-B)^T = A^T - B^T$。
- 对称性验证:通过计算运算后的矩阵转置,判断其是否等于原矩阵。
选项B:当$AB=BA$时,$AB$为对称矩阵
- 计算$(AB)^T$:
$(AB)^T = B^T A^T = BA \quad (\because A,B \text{对称})$ - 验证对称性:
当$AB=BA$时,$(AB)^T = BA = AB$,因此$AB$为对称矩阵。
选项C:$A+B$为对称矩阵
- 计算$(A+B)^T$:
$(A+B)^T = A^T + B^T = A + B \quad (\because A,B \text{对称})$
因此$A+B$为对称矩阵。
选项D:$A-B$为对称矩阵
- 计算$(A-B)^T$:
$(A-B)^T = A^T - B^T = A - B \quad (\because A,B \text{对称})$
因此$A-B$为对称矩阵。
选项E:对任何$n$阶矩阵$P$,$P^TAP$为对称矩阵
- 计算$(P^TAP)^T$:
$(P^TAP)^T = P^T A^T (P^T)^T = P^T A P \quad (\because A \text{对称},\ (P^T)^T = P)$
因此$P^TAP$为对称矩阵。